《2025年细解巧练九年级数学下册北师大版》

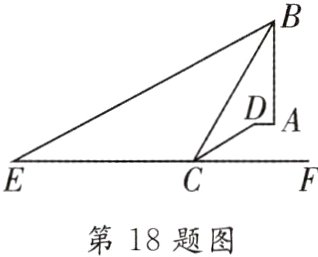
18. [2024·大连二模]如图，某路段路旁有一盏路灯，灯杆AB的正前方有一斜坡CD，已知斜坡CD的长为4 m，坡度i = 1∶$\sqrt{3}$，坡角为∠DCF，灯光受灯罩的影响，最远端的光线BE与地面的夹角∠BEF为28°，最近端的光线BC恰好与地面交于坡面的底端C处，且与地面的夹角∠BCF为60°，AD = 1 m，点A，B，C，D，E，F在同一平面上.
（1）求灯杆AB的长度；（结果保留根号）
（2）求CE的长.（结果精确到0.1 m，参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53，$\sqrt{3}$≈1.73）

答案：
解:
(1)如图,延长BA交CF于点H,过点D 作DG⊥CF于点G.

　
∵i=1:$\sqrt{3}$,坡角为∠DCF,
　
∴tan∠DCF=$\frac{1}{3}$=$\frac{\sqrt{3}}{3}$
　
∴∠DCF=30°.在Rt△CDG中,CD=4,
∴DG=$\frac{1}{2}$CD=2,CG=CD.c0s30°=4×$\frac{√3}{2}$=2√3.
　　由题意可知，四边形DGHA是矩形，
　
∴AD=GH=1,AH=DG=2,
　
∴CH=CG+GH=2$\sqrt{3}$+1.
　在Rt△BCH申,
　∠BCF=60°,CH=2$\sqrt{3}$+1,
　
∴BH=CH.tan60。=(2$\sqrt{3}$+1)×√3
　　　　=6+　　$\sqrt{3}$,
　
∴AB=BH−AH=4+　　$\sqrt{3}$,
　　即灯杆AB的高度为(4+√3)m;
(2)在Rt△BEH中,
　∠BEH=28°,BH=6+√3,
　
∴EH=n≈$\frac{6+\sqrt{3}}{0.53}$≈14.52.
　
∵CH=2$\sqrt{3}$+1,
　
∴CE=EH−CH=14.52−(2$\sqrt{3}$+1)≈10.1,即CE的长约为10.1m.

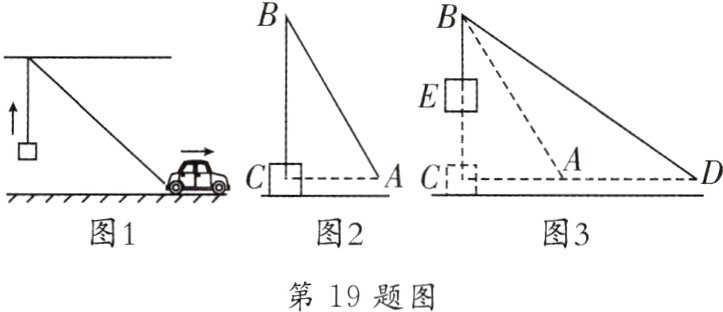
19. [2024·辽宁]如图1，在水平地面上，一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起. 起始位置示意图如图2，此时测得点A到BC所在直线的距离AC = 3 m，∠CAB = 60°；停止位置示意图如图3，此时测得∠CDB = 37°（点C，A，D在同一直线上，且直线CD与平面平行，图3中所有点在同一平面内. 定滑轮半径忽略不计，运动过程中绳子总长不变）.（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，$\sqrt{3}$≈1.73）
（1）求AB的长；
（2）求物体上升的高度CE（结果精确到0.1 m）.

答案： 解:
(1)由题意得∠BCA=90°,
　
∵AC=3,∠CAB=60°,
　
∴在Rt△ABC中,
　
∴AB=cC−²=6m;
　　　　　　　　2
(2)在Rtt△ABC中,由勾股定理得BC=
　　$\sqrt{AB²−AC²}$=3　$\sqrt{3}$,在Rt△BCD中,∠CDB=37°,
　
∴BD=siBnC37°=$\frac{3\sqrt{3}}{0.6}$=5√3,
　
∴BE=BC+AB−BD=3$\sqrt{3}$+6−5$\sqrt{3}$=
　　(6−2$\sqrt{3}$)m,
　
∴CE=BC−BE=3√3−(6−2$\sqrt{3}$)=5√3−6≈2.7(m).
　　答:物体上升的高度约为2.7m.