《2025年细解巧练九年级数学下册北师大版》

11. 如图，在Rt△ABC中，∠CAB = 90°，cosC = $\frac{4}{5}$，AC = 12，BD平分∠CBA交AC边于点D. 求：
（1）线段AB的长；
（2）tan∠DBA的值.

答案：
解:
(1)
∵在Rt△ABC中,∠CAB=90°,
∴cosC=$\frac{AC}{BC}$=$\frac{4}{5}$,
　
∵AC=12,
　
∴BC=15,
　
∴AB=　$\sqrt{152−122}$=9;
(2)过D点作DE⊥BC于点E,
　　设AD=x,则CD=12−x.
　
∵BD平分∠CBA交AC边于
　　点D,∠CAB=90°,
　　　　　　　　　　　　　　
∴DE=AD=r.
　　在Rt△BDE与Rt△BDA中,
　　{BDDE==BDDA,,
　
∴R;△BDE≌Rt△BDA(HL),
　
∴BE=BA=9,
　
∴CE=BC−BE=15−9=6.
　　在Rt△CDE申,
∵∠CED=90°,
　
∴DE²+CE²=CD²,
　
∴x²+6²=(12−x)²,
　　解得x=$\frac{9}{2}$..
∴AD=$\frac{9}{2}$,
　　　　　　　　　　9
　
∴tan∠DBA=$\frac{AD}{AB}$=$\frac{2}{9}$　$\frac{1}{2}$.

12. [2024·温州二模]图1是一款折叠日历，图2是其侧面示意图，若AB = AC = a，BD = CD = b，∠BAC = 20°，∠BDC = 100°，则点A，D之间的距离为 （ ）

A. asin10° - bcos50°
B. acos10° - bsin50°
C. asin10° - bsin50°
D. acos10° - bcos50°

答案： D

13. [2024·东平县一模]如图，将45°的∠AOB按如图所示的方式放置在一把刻度尺上，顶点O与尺下沿的端点重合，OA与尺下沿重合，OB与尺上沿的交点B在尺上的读数为2 cm，若按相同的方式将38°的∠AOC放置在该刻度尺上，则OC与尺上沿的交点C在尺上的读数是______cm.（结果精确到0.1 cm，参考数据：sin38°≈0.62，cos38°≈0.79，tan38°≈0.78）

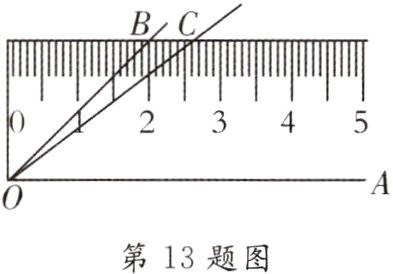
答案： 2.6

14. [2024·槐荫区二模]如图1是《农政全书》中记载有用于采桑的桑梯，图2是示意图. 已知AB = AC = 2米，AC与AB的张角为α，BC为固定张角大小的绳索. 为保证作业安全，α的取值范围大于等于30°且小于等于60°，则BC的最大值为________.

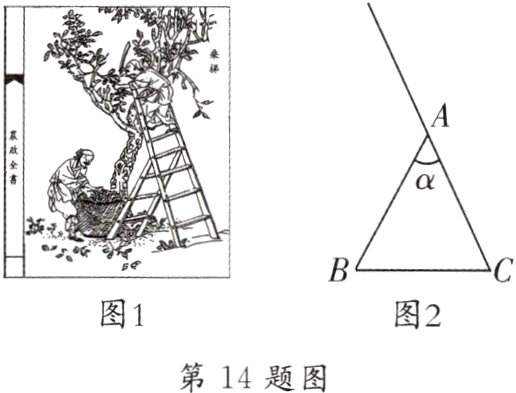
答案： 2米

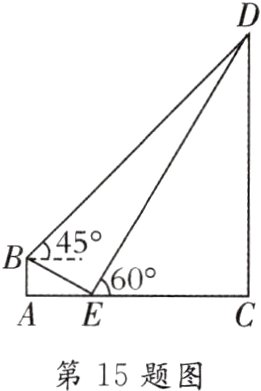
15. [2024·巴中]某兴趣小组开展了测量电线塔高度的实践活动. 如图所示，斜坡BE的坡度i = 1∶$\sqrt{3}$，BE = 6 m，在B处测得电线塔CD顶部D的仰角为45°，在E处测得电线塔CD顶部D的仰角为60°.
（1）求点B离水平地面的高度AB；
（2）求电线塔CD的高度（结果保留根号）.

答案：
解:
(1)
∵斜坡BE的坡度i=1:√3,
　
∴$\frac{AB}{AE}$=$\frac{1}{3}$=$\frac{\sqrt{3}}{3}$,
　
∵tan∠BEA=$\frac{AB}{AE}$=$\frac{\sqrt{3}}{3}$
　
∴∠BEA=30°,
　
∵BE=6m,
　
∴AB=$\frac{1}{2}$BE=3(m);
(2)作BF⊥CD于点F,
　　　　　　
　则四边形ABFC是矩形,AB=CF=3m,
BF=AC,
　设DF=xm,
　在Rt△DBF申,∠DBF=45°,
∴BF=DF=xm,
　在Rt△ABE中,AE=√BE²−AB=
　3√3(m),
　在Rt△DCE中,DC=DF+CF=(x+3)m,∠DEC=60°,
∴EC=DtanC60=((x+3),
∴BF=AE+EC,
∴3√3+(x+3)=x,
∴x=6$\sqrt{3}$+6,
∴电线塔CD的高度为6√3+6+3=
　(6√3+9)m.