《2025年细解巧练九年级数学下册北师大版》

7.[2024·仁寿县模拟]如图，在一笔直的海岸线上有A，B两个码头，A在B的正东方向，一艘小船从A码头沿北偏西60°的方向行驶了30海里到达点P处，此时从B码头测得小船在北偏东45°的方向.则A，B两个码头间的距离为____________（结果保留根号）.

答案： 7.(15+15√3)海里

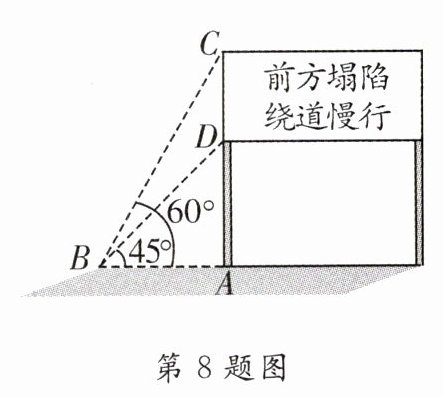
8.[2023·肇庆一模]如图，交警为提醒广大司机前方道路塌陷在路口设立了警示牌.已知立杆AD的高度是3 m，从侧面B点测得警示牌顶端C点和底端D点的仰角分别是60°和45°，那么警示牌CD的高度为_______m.（结果保留根号）

答案： 8.(3√3−3)

9.[2023·武汉模拟]如图，甲、乙两座建筑物的水平距离BC为27 m，从A点测得D点的俯角α为45°，测得C点的俯角β为58°，则乙建筑物的高度CD是________m.（结果根据“四舍五入”法保留整数，参考数据：cos58°≈0.53，tan58°≈1.60）

答案： 9.16

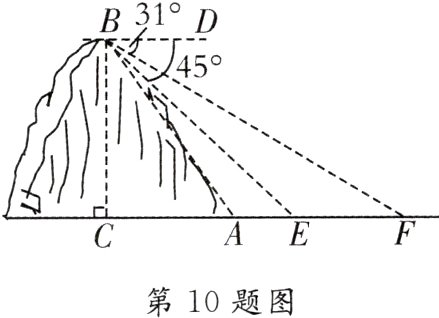
10.[2024·凉州区三模]某镇为创建特色小镇，助力乡村振兴，决定在辖区的一条河上修建一座步行观光桥.如图，河旁有一座小山，山高BC = 80 m，点C，A与河岸E，F在同一水平线上，从山顶B处测得河岸E和对岸F的俯角分别为∠DBE = 45°，∠DBF = 31°.若在此处建桥，求河宽EF的长.（结果精确到1 m，参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）

答案： 10.解:在Rt△BCE中,
BC=80m,∠BEC=∠DBE=45°,
　
∴CE=taBn4C5°=80m.
　在Rt△BCF中,
BC=80m,∠BFC=∠DBF=31°,
　tan∠BFC=$\frac{BC}{CF}$
　
∴$\frac{80}{CF}$≈0.60,
∴CF≈133.3m.
　
∴EF=CF−CE=133.3−80=53.3≈53(m).答:河宽EF的长约为53m.

11.[2023·成都二模]如图，有大树AB和建筑物CD，从建筑物CD的顶部D处看树顶A处的仰角为45°，看树干E处的俯角为37°.若B，C在同一水平地面上，已知BC = 12米，BE = 2米.求大树的高度AB.（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

答案：
11.解:过点D作DF⊥AB，垂足为点F,
　　　　　　　
　由题意,得DF=BC=12米.
　在Rt△ADF中,∠ADF=45°,
∴AF=DF.tan45°=12(米).
　　在Rt△DFE中,∠EDF=37,
　
∴EF=DF.tan37°≈12×0.75=9(米).
　　又
∵BE=2米,
　
∴AB=AF+EF+BE=12+9+2=23(米).
∴大树的高度AB约为23米.