《2025年点拨训练七年级数学下册华师大版》

1.[2024·泉州期末]如图所示的四个交通标志图中，为旋转对称图形的是（ ）

答案： 1.D

2.下列图形中，是轴对称图形但不是旋转对称图形的是（ ）

答案： 2.B

3.[2024·长春期末]风力发电机可以在风力作用下发电，如图的叶片图案绕中心旋转后能与原来的图案重合，则至少要旋转（ ）

A.60°
B.120°
C.180°
D.270°

答案： 3.B

4.如图是几种汽车轮毂图案，图案围绕中心旋转90°后能与原来的图案重合的是（ ）

答案： 4.B

5.下列旋转对称图形，分别绕哪个点至少旋转多少度才能与原图形重合？（点在图上画出）

答案： 解:画图略.
　题图①至少旋转60°;题图②至少旋转72°;题图③至少旋转40°.

6.将一个正n边形旋转90°或120°后，均能与自身重合，则n可以为________.（写出一个即可）

答案： 6.12(答案不唯一)

7.[2024·周口期末]如图，图案由五个相同的叶片组成，其绕点O旋转72°后可以和自身重合，若五个叶片的总面积为20，∠AOB = 72°，则图中阴影部分的面积为________.

答案： 7.4

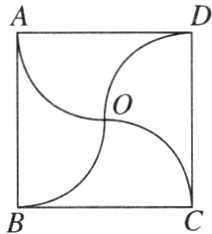
8.[2024·郑州月考]如图，正方形ABCD的边长为2 cm，以各边中点为圆心，1 cm为半径依次作$\frac{1}{4}$圆，将正方形分成四部分.
（1）这个图形是旋转对称图形，旋转中心是点________，最小旋转角是________度.
（2）求图形OBC的周长和面积.

答案： 解:
(1)0；90
(2)图形OBC的周长=BC+ $\frac{1}{2}$圆的周长=2+ $\frac{1}{2}$×2π×1=(2+π)cm，
　图形OBC的面积= $\frac{1}{4}$$S_{正方形ABCD}$= $\frac{1}{4}$×2×2=1(cm²)，即图形OBC的周长为(2+π)cm，面积为1cm².

9.如图，正方形ABCD与正方形EFGH边长相等，下列说法：①此图可看成由正方形ABCD绕点O旋转45°前后的图形组成；②此图可看成由△ABC绕点O分别旋转45°，90°，135°，180°，225°前后的图形组成；③此图可看成由△BOC绕点O分别旋转45°，90°，135°，225°，250°前后的图形组成.正确的有________.（填序号）

答案： 9.①②