《2025年点拨训练七年级数学下册华师大版》

12. 若a＞b，c＜0，则下列正确的是 （ ）
A. a + c＞b
B. a + c＞b - c
C. ac - 1＞bc - 1
D. a(c - 1)＜b(c - 1)

答案： D

13. [2024·南阳新野期末] 已知a - 2＞0，则下列选项正确的是 （ ）
A. - 2＜ - a＜a＜2
B. - a＜ - 2＜a＜2
C. - a＜ - 2＜2＜a
D. - 2＜ - a＜2＜a

答案： C

14. 新考法 设●、▲、■表示三种不同的物体，现用天平称了两次，情况如图所示，那么●、▲、■这三种物体按质量从大到小的顺序排列为 （ ）
　　　　　
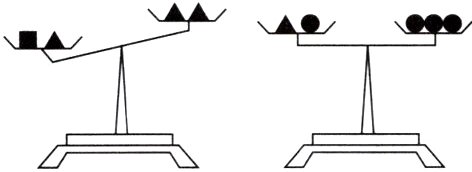
A. ■、▲、●
B. ■、●、▲
C. ▲、●、■
D. ▲、■、●

答案： A

15. [2024·淮南期末] 某人从一个鱼摊上买了三条鱼，平均每条a元，又从另一个鱼摊上买了两条鱼，平均每条b元，后来他又以每条$\frac{a + b}{2}$元的价格把鱼全部卖给了乙，结果发现赔了钱，原因是 （ ）
A. a＞b
B. a＜b
C. a = b
D. 与a、b的大小无关

答案： A

16. [2024·南阳期中] 若x + y＜0，且(m - 1)x＞(1 - m)y，则m的值可以是______.

答案： 0(答案不唯一)

【变式题】已知关于x的不等式mx - 2≤0的解集是x≥$\frac{2}{m}$，则m的取值范围是______.

答案： m ＜ 0

17. 在学习不等式的基本性质时，张老师给出以下两个说法：
①若m＞n，则m²＞n²；
②若a＜b，c＜d，则a - c＜b - d.
其中错误的是______（填序号）.

答案： ①②

18. 原创题 已知b＞a＞0，c＞0，请判断$\frac{b + c}{a + c}$＞$\frac{b}{a}$是否正确，并说明理由.

答案： 解：不正确.理由如下：因为b ＞ a ＞ 0，c ＞ 0，
所以bc ＞ ac，a + c ＞ 0，所以ab + bc ＞ ab + ac，
即b(a + c) ＞ a(b + c)，
所以b ＞ $\frac{a(b + c)}{a + c}$，所以$\frac{b}{a}$ ＞ $\frac{b + c}{a + c}$，即$\frac{b + c}{a + c}$ ＜ $\frac{b}{a}$.
所以原式不正确.

19. [运算能力] 根据等式和不等式的基本性质，我们可以得到比较两数大小的方法：若a - b＞0，则a＞b；若a - b = 0，则a = b；若a - b＜0，则a＜b. 反之也成立. 这种比较大小的方法称为“求差法”. 请运用这种方法尝试解决下面的问题：
(1)比较4 + 3a² - 2b + b²与3a² - 2b + 1的大小；
(2)若2a + 2b＞3a + b，比较a，b的大小.

答案： 解：
(1)因为4 + 3a²－2b + b²－(3a²－2b + 1)=b² + 3 ＞ 0，所以4 + 3a²－2b + b² ＞ 3a²－2b + 1.
(2)因为2a + 2b ＞ 3a + b，
所以(2a + 2b)－(3a + b)=－a + b ＞ 0，
∴a ＜ b.