《2025年点拨训练七年级数学下册华师大版》

1. [2024·郑州期末] 2024年6月，我国选手苗浩以7小时58分4秒的成绩创造了亚洲“大铁”新纪录，将该记录用时记为t₀，若今后的选手要打破该记录，则比赛用时t的取值范围为（ ）
A. t＞t₀
B. t＜t₀
C. t≥t₀
D. t≤t₀

答案： B

2. x = 3是下列哪个不等式的一个解？（ ）
A. x - 1＜0
B. x + 1＜4
C. 2x - 3＞4
D. 2x + 3＜10

答案： D

3. [2024·眉山期中] 下列各式：①x² + 2＞5；②a + b；③$\frac{x}{3}$≥$\frac{2x - 1}{5}$；④x - 1；⑤x + 2≤3，其中是一元一次不等式的有（ ）
A. 2个
B. 3个
C. 4个
D. 5个

答案： A

4. [2024·长春期末] 不等式3x + 1＞4的解集在数轴上表示正确的是（ ）

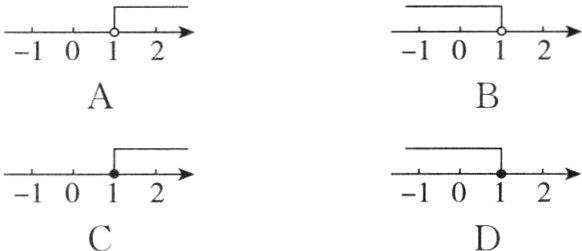
答案： A

5. [2024·重庆期中] 已知a＜b，则下列各式中一定成立的是（ ）
A. a - b＞0
B. ac²＞bc²
C. $\frac{a}{2}$ - 1＞$\frac{b}{2}$ - 1
D. -3a＞-3b

答案： D

6. [2024·北京期末] 定义新运算“*”，规定a*b = a - 2b. 若关于x的不等式x*m＞5的解集为x＞ - 1，则m的值为（ ）
A. -1
B. -3
C. 2
D. 3

答案： B

7. 一种电子琴每台进价为1800元，如果商店按标价的八折出售，所得利润仍不低于实际售价的10％，那么每台电子琴的标价x（元）的范围是（ ）
A. x≥2500
B. x≥2475
C. x≤2500
D. x≤2475

答案： A

8. 已知$\begin{cases}x = -2\\y = 5\end{cases}$是不等式kx + 2y≤4的一个解，则整数k的最小值为（ ）
A. 3
B. -3
C. 4
D. -4

答案： A

9. 用不等式表示“a（a≠0）的倒数与2的差是非负数”：________.

答案： $\frac{1}{a}-2\geq0$

10. 若a＞b，c＞d，则a - d________b - c.

答案： ＞

11. [2024·烟台中考] 关于x的不等式m - $\frac{x}{2}$＜1 - x有正数解，m的值可以是________（写出一个即可）.

答案： 0(答案不唯一)

12. [2024·合肥期中] 如图是由灰白两种正方形地砖拼成的图案，每块正方形地砖的边长为0.6 m. 用Lₙ表示第n个图案的水平长度，要使Lₙ不小于72 m，至少需要________块灰色地砖.

答案： 60　点拨:观察题图可得$L_{n}=0.6\times(2n + 1)\text{m}$，由题意可知$0.6\times(2n + 1)\geq72$，解得$n\geq\frac{119}{2}$，因为$n$为正整数，所以$n$的最小值为60，易知第$n$个图案中有$n$块灰色地砖，所以至少需要灰色地砖60块.

13. 若|2a - 6|＞6 - 2a，则a的取值范围是________.

答案： $a＞3$

14. [2024·驻马店期中] 解下列不等式，并把它们的解集在数轴上表示出来：
（1）3(1 - 3x) - 2(4 - 2x)≥0；
（2）$\frac{x - 1}{3}$＜$\frac{x - 3}{12}$ + 1.

答案：
解:
(1)去括号,得$3 - 9x - 8 + 4x\geq0$，
　移项,得$-9x + 4x\geq8 - 3$，合并同类项,得$-5x\geq5$，
　两边同时除以$-5$，得$x\leq - 1$.
　在数轴上表示出解集如图①.
　
(2)去分母,得$4(x - 1)＜(x - 3)+12$，
　去括号,得$4x - 4＜x - 3 + 12$，
　移项,得$4x - x＜ - 3 + 12 + 4$，
　合并同类项，得$3x＜13$，
　两边同时除以3,得$x＜\frac{13}{3}$.
　在数轴上表示出解集如图②.