《2025年点拨训练七年级数学下册华师大版》

11. [2024·驻马店期末] 如果一个多边形的每一个外角都是72°，那么这个多边形的内角和为________.

答案： 540°

12. 在下列正多边形组合中，不能铺满地面的是 （ ）
A. 正八边形和正方形
B. 正五边形和正八边形
C. 正六边形和正三角形
D. 正三角形和正方形

答案： B

13. [2024·白山期末] 如图，在△ABC中，∠B = ∠C = 60°，将△BDE沿直线DE翻折，使点B落在B₁处，DB₁，EB₁分别交边AC于点F，G. 若∠ADF = 80°，则∠GEC = ________.
　　　 　　

答案： 40°

14. 如图为两直线a，b与△ABC相交的情形，其中a，b分别与BC，AB平行. 根据图中标示的角度，回答下列问题：

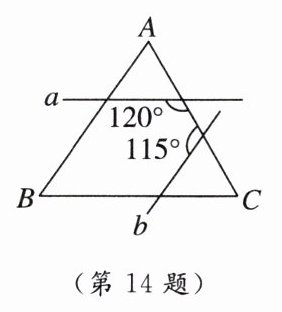
(1)a与b所夹锐角的度数为________；
(2)∠B的度数为________.

答案：
(1)55°
(2)55°

15. [几何直观]正五边形GHCDL按如图所示的方式叠放在正六边形ABCDEF上，CD边互相重合，延长LG交AF于点P，则∠APG的度数为________.
　　　　　　　　　　　　　　

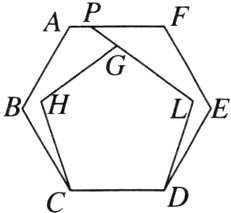
答案： 144°

16. [2024·宁波月考] 在社会实践手工课上，小明同学设计了如图这样一个零件，如果∠A = 52°，∠B = 25°，∠C = 30°，∠D = 35°，∠E = 72°，那么∠F = ________.
　　　　

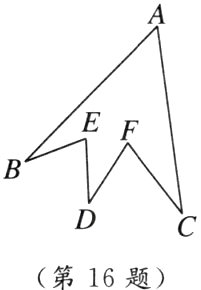
答案： 70

17. [2024·重庆期中] 如图，在△ABC中，AB = AC，BD是边AC上的中线，BD把原三角形的周长分为15和9两部分，则腰AB的长为________.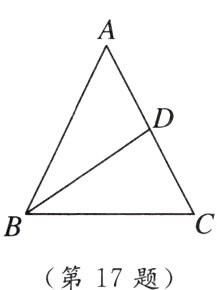

答案： 10

18. [2024·泉州期中] 若等腰三角形的周长为18，一边为4，则腰的长度为________.

答案： 7

19. 将一个五边形纸片剪去一个角后得到的另一个多边形的内角和是________.

答案： 360°或540°或720°

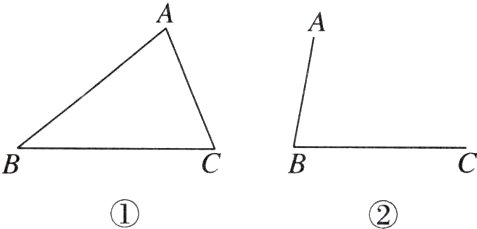
20. [2024·南阳期中] 我们已经学过三角形的内角和为180°，即如图①，在△ABC中，∠A + ∠B + ∠C = 180°. 如果三角形两个内角α与β满足2α + β = 90°，那么我们称这样的三角形为“准直角三角形”. 如图②，∠ABC = 80°，若点P是射线BC上一点，且△ABP是“准直角三角形”，则∠APB = ________.
　　　　　　　　

答案： 5°或95° 点拨：设∠ABP=α=80°，
∴160°+β=90°，解得β=-70°(舍去)；
设∠BAP=α，∠APB=β，
∴α+β+80°=180°，2α+β=90°，
解得α=-10°，β=110°(舍去)；
设∠BAP=α，∠ABP=β=80°，
∴2α+80°=90°，解得α=5°，
∴∠APB=180° - 80° - 5°=95°；
设∠APB=α，∠ABP=β=80°，
∴2α+80°=90°，解得α=5°，
∴∠APB=5°；
设∠APB=α，∠BAP=β，
∴2α+β=90°，α+β+80°=180°，
解得α=-10°，β=110°，(舍去).
综上所述，∠APB=5°或∠APB=95°.