《2025年点拨训练七年级数学下册华师大版》

1. [2024·眉山期中]下列式子：①$-3＜0$；②$2x + 3y\geqslant0$；③$x = 1$；④$x^{2}-2xy + y^{2}$；⑤$x＞2$；⑥$x + 1＞3$.其中不等式有 （ ）
A. 3个
B. 4个
C. 5个
D. 6个

答案： B

2.若$(m + 1)x^{|m + 2|}+4＜0$是关于$x$的一元一次不等式，则$m$的值为 （ ）
A. -1
B. -3
C. -2
D. -3或-1

答案： B

3.下列是一元一次不等式组的是 （ ）
A.$\begin{cases}x + 3＜2,\\\frac{1}{x}+2\geqslant5\end{cases}$
B.$\begin{cases}x + y＞4,\\x - y＜6\end{cases}$
C.$\begin{cases}x + 4\geqslant - 3,\\6y＜12\end{cases}$
D.$\begin{cases}x - 6＞-2,\\x + 1＜8\end{cases}$

答案： D

4.下列说法中，正确的是 （ ）
A.$x = 1$是不等式$3x＞5$的解
B.$x = 2$是不等式$3x＞5$的唯一解
C.$x = 2$是不等式$3x＞5$的解集
D.$x = 2$是不等式$3x＞5$的一个解

答案： D

5. [2024·浙江中考]不等式组$\begin{cases}2x - 1\geqslant1,\\3(2 - x)＞-6\end{cases}$的解集在数轴上表示为 （ ）

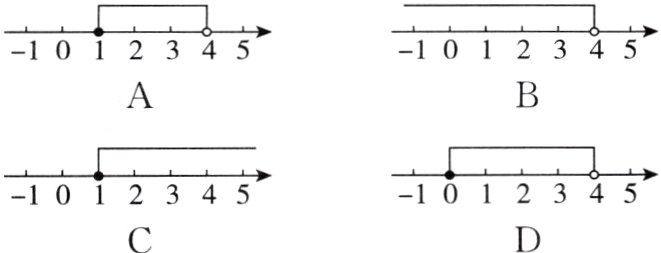
答案： A

6. [2024·广州中考]若$a＜b$，则 （ ）
A.$a + 3＞b + 3$
B.$a - 2＞b - 2$
C.$-a＜-b$
D.$2a＜2b$

答案： D

7. [2024·达州期末]若$a＞3$，则$|6 - 2a|=$______（用含$a$的式子表示）.

答案： 2a - 6

8. [2024·湖州长兴期中]请根据不等式的性质填空：
问题：若$x＞3y$，$y＞a$，$2a - 4＞0$，试求$x$的取值范围.
解：$\because2a - 4＞0$，$\therefore2a＞4$（理由：不等式的基本性质1）.
$\therefore a＞2$（理由：______________）.
$\because y＞a$，$\therefore y＞2$（理由：______________），
$\therefore3y＞$______（理由：______________）.
$\because x＞3y$，$\therefore x＞$______（理由：______）.

答案： 不等式的基本性质2;不等式的传递性;6;不等式的基本性质2;6;不等式的传递性

9. [2024·眉山中考]解不等式：$\frac{x + 1}{3}-1\leqslant\frac{2 - x}{2}$，并把它的解集表示在数轴上.
　　　　−5−4−3−2−1012345

答案：
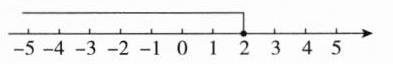
解:$\frac{x + 1}{3}-1\leqslant\frac{2 - x}{2}$，
去分母，得2(x + 1) - 6≤3(2 - x)，
去括号，得2x + 2 - 6≤6 - 3x，
移项，得2x + 3x≤6 + 6 - 2，
合并同类项，得5x≤10，
两边都除以5，得x≤2，
其解集在数轴上表示如图.

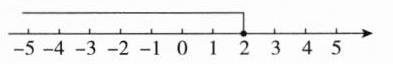
10.解不等式组：$\begin{cases}2x + 1\geqslant x + 2,①\\2x - 1＜\frac{1}{2}(x + 4).②\end{cases}$

答案： 解:解不等式①，得x≥1，解不等式②，得x＜2，
所以不等式组的解集是1≤x＜2.