《2025年点拨训练七年级数学下册华师大版》

15. [2024·长春南关区期中] 当x取何正整数时，代数式$\frac{x + 3}{2}$与$\frac{2x - 1}{3}$的值的差大于1？

答案： 解:根据题意，得$\frac{x + 3}{2}-\frac{2x - 1}{3}＞1$，解得$x＜5$.
　所以当$x$取正整数1,2,3,4时，代数式$\frac{x + 3}{2}$与$\frac{2x - 1}{3}$的值的差大于1.

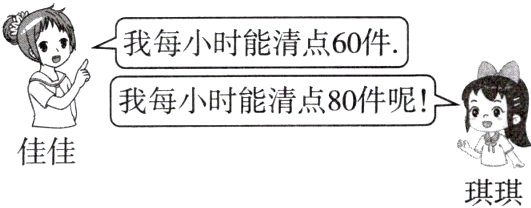
16. [2024·鹤壁期中] 学校体育馆为提升学生健康运动质量，需要更新馆内老旧运动器材，现安排佳佳和琪琪接替完成300件器材的清点工作，如图是两人的对话. 若两人需在4 h内清点完所有器材，琪琪至少要清点多少件？

答案： 解:设琪琪要清点$x$件器材，则佳佳要清点$(300 - x)$件器材.
　根据题意，得$\frac{300 - x}{60}+\frac{x}{80}\leq4$，解得$x\geq240$.
　答:琪琪至少要清点240件器材.

17. [2024·四平铁西区期末] 若关于x，y的方程组$\begin{cases}2x + 3y = -m\\3x + 5y = 3m - 8\end{cases}$的解满足x + 2y≤2，求m的取值范围.

答案： 解:$\begin{cases}2x + 3y = - m,①\\3x + 5y = 3m - 8,②\end{cases}$
　② - ①,得$x + 2y = 4m - 8$.
　因为$x + 2y\leq2$，所以$4m - 8\leq2$，
　解得$m\leq\frac{5}{2}$.

18. [2024·南通中考] 某快递企业为提高工作效率，拟购买A，B两种型号智能机器人进行快递分拣. 相关信息如下：
信息一

信息二

（1）求A，B两种型号智能机器人的单价；
（2）该企业准备用不超过700万元购买A，B两种型号智能机器人共10台，则该企业选择哪种购买方案，能使每天分拣快递的件数最多？

答案： 解:
(1)设A型机器人的单价为$x$万元，B型机器人的单价为$y$万元，根据题意，得$\begin{cases}x + 3y = 260,\\3x + 2y = 360,\end{cases}$
解得$\begin{cases}x = 80,\\y = 60.\end{cases}$
答:A型机器人的单价为80万元，B型机器人的单价为60万元.
(2)设购买A型机器人$a$台，则购买B型机器人$(10 - a)$台，
根据题意，得$80a + 60(10 - a)\leq700$，
所以$a\leq5$.
因为每天分拣快递的件数为$22a + 18(10 - a)=4a + 180$，
所以当$a = 5$时，每天分拣快递的件数最多，为$4\times5 + 180 = 200$，
所以选择购买A型机器人5台，购买B型机器人5台，能使每天分拣快递的件数最多.