第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1. 新考法 某药店用3000元购进甲、乙两种体温计,体温计卖出后,甲种体温计的利润率是25%,乙种体温计的利润率是20%,两种体温计共获利675元,若甲种体温计的进价为每支2元,乙种体温计的进价为每支5元,则甲、乙两种体温计共购进______支.
答案:
1050
2. 新考法 [2024·郑州开学考] 佳佳坐在匀速行驶的车上,将每隔一段时间看到的里程碑上的数描述如下:
|时刻|12:00|13:00|14:00|
|--|--|--|--|
|里程碑上的数|是一个两位数,数字之和为7|十位数字和个位数字与12:00看到的刚好相反|比12:00看到的两位数中间多了个0|
则佳佳12:00看到的两位数是______.
|时刻|12:00|13:00|14:00|
|--|--|--|--|
|里程碑上的数|是一个两位数,数字之和为7|十位数字和个位数字与12:00看到的刚好相反|比12:00看到的两位数中间多了个0|
则佳佳12:00看到的两位数是______.
答案:
16
3. 教材改编题 如图,一列快车长70 m,一列慢车长80 m,若两车同向而行,快车从追上慢车到完全超过慢车,所用时间为20 s. 若两车相向而行,则两车从相遇到完全分离所用的时间为4 s,求两车每秒钟各行多少米.
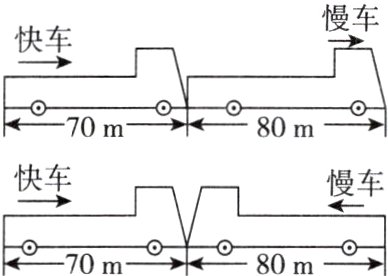

答案:
解:设快车每秒行x m,慢车每秒行y m,根据题意,得$\begin{cases}20x - 20y = 70 + 80 \\ 4x + 4y = 70 + 80 \end{cases}$,解得$\begin{cases}x = 22.5 \\ y = 15 \end{cases}$
答:快车每秒行22.5 m,慢车每秒行15 m.
答:快车每秒行22.5 m,慢车每秒行15 m.
4. 甲、乙两工程队共同修建150 km的公路,原计划30个月完工. 实际施工时,甲队通过技术创新,施工效率提高了50%,乙队施工效率不变,结果提前5个月完工. 甲、乙两工程队原计划平均每月分别修建多长?
答案:
解:设甲工程队原计划平均每月修建x km,乙工程队原计划平均每月修建y km,根据题意,得$\begin{cases}x + y = \frac{150}{30} \\ (1 + 50\%)x + y = \frac{150}{30 - 5} \end{cases}$,解得$\begin{cases}x = 2 \\ y = 3 \end{cases}$
答:甲工程队原计划平均每月修建2 km,乙工程队原计划平均每月修建3 km.
答:甲工程队原计划平均每月修建2 km,乙工程队原计划平均每月修建3 km.
5. [2024·周口商水期中] 已知用2辆A型车和1辆B型车载满货物一次可运货10 t;用1辆A型车和2辆B型车载满货物一次可运货11 t. 某物流公司现有31 t货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物,根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案,并把符合要求的租车方案都列出来.
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次,则(2)中最省钱的租车方案是____________________,最少租车费为______元.
(1)1辆A型车和1辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案,并把符合要求的租车方案都列出来.
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次,则(2)中最省钱的租车方案是____________________,最少租车费为______元.
答案:
解:
(1)设1辆A型车和1辆B型车都载满货物一次可分别运货x t,y t,
依题意,得$\begin{cases}2x + y = 10 \\ x + 2y = 11 \end{cases}$,解得$\begin{cases}x = 3 \\ y = 4 \end{cases}$
答:1辆A型车载满货物一次可运货3 t,1辆B型车载满货物一次可运货4 t.
(2)由
(1)得,$3a + 4b = 31$,$\therefore a = \frac{31 - 4b}{3}$
$\because a$,$b$都是正整数,$\therefore \begin{cases}a = 9 \\ b = 1 \end{cases}$或$\begin{cases}a = 5 \\ b = 4 \end{cases}$或$\begin{cases}a = 1 \\ b = 7 \end{cases}$
即有3种租车方案:
方案一:租A型车9辆,B型车1辆;
方案二:租A型车5辆,B型车4辆;
方案三:租A型车1辆,B型车7辆.
(3)租A型车1辆,B型车7辆;940
(1)设1辆A型车和1辆B型车都载满货物一次可分别运货x t,y t,
依题意,得$\begin{cases}2x + y = 10 \\ x + 2y = 11 \end{cases}$,解得$\begin{cases}x = 3 \\ y = 4 \end{cases}$
答:1辆A型车载满货物一次可运货3 t,1辆B型车载满货物一次可运货4 t.
(2)由
(1)得,$3a + 4b = 31$,$\therefore a = \frac{31 - 4b}{3}$
$\because a$,$b$都是正整数,$\therefore \begin{cases}a = 9 \\ b = 1 \end{cases}$或$\begin{cases}a = 5 \\ b = 4 \end{cases}$或$\begin{cases}a = 1 \\ b = 7 \end{cases}$
即有3种租车方案:
方案一:租A型车9辆,B型车1辆;
方案二:租A型车5辆,B型车4辆;
方案三:租A型车1辆,B型车7辆.
(3)租A型车1辆,B型车7辆;940
查看更多完整答案,请扫码查看


