第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
8. [2024·洛阳期中] 如图,一个瓶子的容积为1.9 L,瓶内装着一些溶液,当瓶子正放时,瓶内溶液的高度为15 cm,倒放时,空余部分的高度为4 cm. 则瓶内溶液的体积是( )
A. 1.8 L B. 1.3 L C. 1.5 L D. 1.9 L
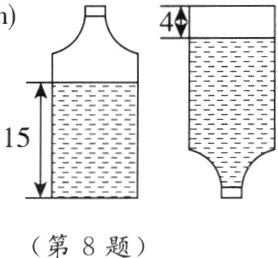
A. 1.8 L B. 1.3 L C. 1.5 L D. 1.9 L

答案:
C
9. (新考法) 如图,一个无盖长方体容器的内底面长为8 cm,宽为6 cm,高为16 cm,容器中水的高度为2 cm,现把一块棱长为4 cm的立方体金属块放入水中,则容器内的水将升高______cm.
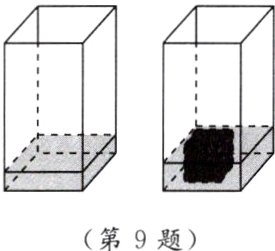

答案:
1
10. [2024·漯河期末] 如图,在长方形ABCD中放入六个完全相同的小长方形,则图中阴影部分的面积之和为________.
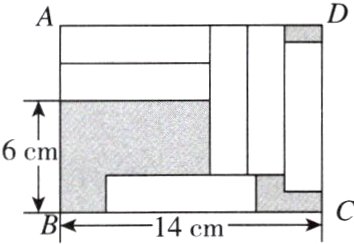

答案:
44 cm²
11. (新情境) [2024·福州仓山区期中] 如图是某农场的长方形猪棚. 其中一面靠墙,其他三面全部用围栏围住,已知三面围栏总长为13.8 m,猪棚的长AB比宽BC多6 m,且BC上有一扇1.2 m宽的门,围栏衔接处的长度忽略不计. 求该猪棚的面积.
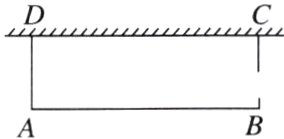

答案:
解:设猪棚的长为x m,则猪棚的宽为(x - 6)m,
根据题意,得x+(x - 6)+(x - 6 - 1.2)=13.8,
解得x = 9,所以x - 6 = 9 - 6 = 3,
所以该猪棚的面积为9×3 = 27(m²).
根据题意,得x+(x - 6)+(x - 6 - 1.2)=13.8,
解得x = 9,所以x - 6 = 9 - 6 = 3,
所以该猪棚的面积为9×3 = 27(m²).
12. [2024·德州期末] 如图是某长方体包装盒的展开图,具体数据如图所示,且长方体盒子的长是高的2倍.
(1)设长方体的高为x cm,则长为________cm,宽为________cm;(用含x的式子表示)
(2)请求出长方体包装盒的体积.
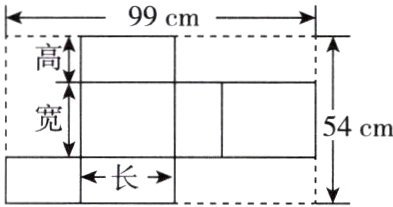
(1)设长方体的高为x cm,则长为________cm,宽为________cm;(用含x的式子表示)
(2)请求出长方体包装盒的体积.

答案:
解:
(1)2x;(54 - 2x)
(2)由展开图,得4x+(54 - 2x)+x = 99,
解得x = 15,所以2x = 30,54 - 2x = 24,
所以长方体包装盒的体积为30×24×15 = 10 800(cm³).
(1)2x;(54 - 2x)
(2)由展开图,得4x+(54 - 2x)+x = 99,
解得x = 15,所以2x = 30,54 - 2x = 24,
所以长方体包装盒的体积为30×24×15 = 10 800(cm³).
13. (新题型) 如图,甲、乙两个长方体透明容器放置在同一水平桌面上,甲中盛满水,底面积为80 dm²,高为6 dm;乙中没有水,底面积为40 dm²,高为9 dm. 从甲向乙每分钟注水30 dm³.
(1)甲中水面的高度每分钟下降________dm,乙中水面的高度每分钟上升________dm;
(2)从开始注水起,经过________min,两个容器中水面的高度相差3 dm.
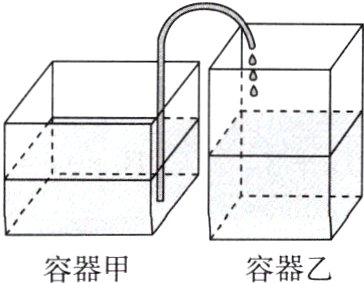
(1)甲中水面的高度每分钟下降________dm,乙中水面的高度每分钟上升________dm;
(2)从开始注水起,经过________min,两个容器中水面的高度相差3 dm.

答案:
(1)$\frac{3}{8}$;$\frac{3}{4}$
(2)$\frac{8}{3}$或8 点拨:设经过x min,两个容器中水面的高度相差3 dm,根据题意得,甲中水面的高度为$(6 - \frac{3}{8}x)$dm,乙中水面的高度为$\frac{3}{4}x$dm,当$6 - \frac{3}{8}x - \frac{3}{4}x = 3$时,解得$x = \frac{8}{3}$;当$\frac{3}{4}x - (6 - \frac{3}{8}x)=3$时,解得x = 8.故经过$\frac{8}{3}$min或8 min,水面的高度相差3 dm.
(1)$\frac{3}{8}$;$\frac{3}{4}$
(2)$\frac{8}{3}$或8 点拨:设经过x min,两个容器中水面的高度相差3 dm,根据题意得,甲中水面的高度为$(6 - \frac{3}{8}x)$dm,乙中水面的高度为$\frac{3}{4}x$dm,当$6 - \frac{3}{8}x - \frac{3}{4}x = 3$时,解得$x = \frac{8}{3}$;当$\frac{3}{4}x - (6 - \frac{3}{8}x)=3$时,解得x = 8.故经过$\frac{8}{3}$min或8 min,水面的高度相差3 dm.
查看更多完整答案,请扫码查看


