《2025年点拨训练七年级数学下册华师大版》

1. [2024·长春期中]下列各组长度的线段能组成三角形的是（ ）
A. 1 cm，2 cm，3 cm
B. 4 cm，5 cm，10 cm
C. 3 cm，3 cm，6 cm
D. 5 cm，6 cm，8 cm

答案： D

2. 如图，在△ABC中，∠A = 35°，∠B = 25°，则∠ACD的度数是（ ）
A. 60° B. 55° C. 120° D. 65°
　　　

答案： A

3. [2024·郑州期末]在△ABC中，下列作辅助线的方法不能说明三角形的内角和为180°的是（ ）

答案： D

4. 如图，工人师傅做了一个长方形窗框ABCD，E、F、G、H分别是四条边上的中点，为使它稳固，需要在窗框上钉一根木条，则这根木条可以钉在（ ）
A. B、D两点之间 B. E、G两点之间
C. F、H两点之间 D. A、B两点之间
　　　

答案： A

5. [2024·太原期中]如图，在△ABC中，AD是高，AE是角平分线，AF是中线. 则下列结论错误的是（ ）
A. BF = CF
B. ∠BAE = ∠EAC
C. ∠C + ∠CAD = 90°
D. S△BAE = S△EAC
　　　　　　　　　　　　

答案： D

6. [2024·黄冈月考]如图，三角形纸片ABC中，∠A = 65°，∠B = 70°，将∠C沿DE折叠，使点C落在△ABC外的点C′处，若∠1 = 20°，则∠2的度数为（ ）
A. 80° B. 90° C. 100° D. 110°
　　

答案： D

7. 如图，为估测池塘两岸A，B间的距离，在其一侧取点P，测得PA = 15 m，PB = 9 m，则A，B间的距离可能是________.（写出一个即可）

答案： 20 m(答案不唯一)

8. 如图，AD是△ABC中边BC上的中线，E，F分别是AB，AD的中点，若△ACD的面积为12 cm²，则△DEF的面积为________ cm².
　　　

答案： 3

9. 如图，AB//CD，AC平分∠BAD，DB平分∠ADC，AC和DB交于点E，则图中共有________个直角三角形.
　　

答案： 3

10. [2024·厦门期中]如图，在△ABC中，AB = AC = 2，P是BC上任意一点，PE⊥AB于点E，PF⊥AC于点F. 若S△ABC = 1，则PE + PF = ________.
　　

答案： 1

11. 小明将一副三角尺按如图的方式叠放在一起，∠ACE ＜ 180°且点E在直线AC的上方，若三角尺BCE有一条边与斜边AD平行，则∠ACE = ________.
　　

答案： 15°或60°或150°

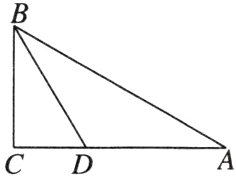
12. [2024·北京期中]如图，在△ABC中，BD是角平分线，且∠ABD = ∠A，∠C = 3∠A.
（1）求△ABC各内角的度数；
（2）求∠ADB的度数.
　　　　　　　　　　　　　　

答案： 解:
(1)
∵BD平分∠ABC,∠ABD = ∠A,
∴∠ABD = ∠CBD = ∠A.
∵∠C = 3∠A,∠A + ∠C + ∠ABC = 180°,
∴∠A + 3∠A + 2∠A = 180°,
∴∠A = 30°,
∴∠ABC = 60°,∠C = 90°.
(2)
∵∠A = ∠ABD = 30°,
∴∠ADB = 180° - 30° - 30° = 120°.