《2025年海淀单元测试AB卷七年级数学下册鲁教版》

$6.$如图，在$△ABC$中，$AE$是$∠BAC$的平分线，$AE = BE，$外角$∠ACD = 120°，$则$∠AEC$的度数为$( )$
$A.85° B.80° C.75° D.70°$
$　　　　$$ 　　　$

答案： B

7.[几何直观]如图，如果可以在三个完全相同的正方形拼成的图案中随意取点，那么这个点取在阴影部分的概率是( )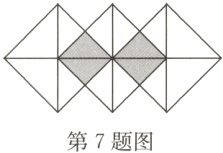
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{5}$
D.$\frac{1}{6}$

答案： C

8.直线l1：y = x - 4与直线l2：y = -$\frac{4}{3}$x + 3相交于点(3，-1)，则方程组$\begin{cases}\frac{x}{2}-\frac{y}{2}=2\\x+\frac{3y}{4}=\frac{9}{4}\end{cases}$的解是( )
A.$\begin{cases}x = 3\\y = -1\end{cases}$
B.$\begin{cases}x = -1\\y = 3\end{cases}$
C.$\begin{cases}x = -1\\y = -3\end{cases}$
D.$\begin{cases}x = 3\\y = 1\end{cases}$

答案： A

$9.$如图，$AB//CD//EF，$下列各式中，正确的是$( )$
$A.∠1 + ∠2 + ∠3 = 180° B.∠1 + ∠2 - ∠3 = 90°$
$C.∠1 - ∠2 + ∠3 = 90° D.∠2 + ∠3 - ∠1 = 180°$
$　$$ 　　　$

答案： D [解析]
∵AB//CD//EF，
∴∠2 + ∠BOE = 180°，∠3 = ∠COE. 又∠BOE = ∠COE - ∠1，
∴∠2 + ∠3 - ∠1 = 180°. 故选 D.

10.[模型观念]在长为20 m、宽为16 m的长方形空地上，沿平行于长方形各边的方向割出三个完全相同的小长方形花圃(阴影部分)，其示意图如图所示，则花圃的总面积是( )$ 　　$
A.64 m²
B.32 m²
C.128 m²
D.96 m²

答案： D [解析]设小长方形的长为 x m，宽为 y m. 由题意，得$\begin{cases}2x + y = 20\\2y + x = 16\end{cases}$，解得$\begin{cases}x = 8\\y = 4\end{cases}$，即小长方形的长为 8 m，宽为 4 m. 所以一个小长方形花圃的面积是 32 m²，花圃的总面积是 96 m². 故选 D.

11.如图，在△ABC中，AB = AC，BD = CE，BE = CF.若∠A = 50°，则∠DEF =( )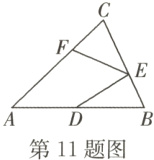
A.55°
B.60°
C.65°
D.70°

答案： C [解析]
∵AB = AC，
∴∠B = ∠C. 在△DBE 和△ECF 中，$\begin{cases}BD = CE\\∠B = ∠C\\BE = CF\end{cases}$，
∴△DBE≌△ECF（SAS），
∴∠EFC = ∠DEB.
∵∠A = 50°，
∴∠C = (180° - 50°)÷2 = 65°，
∴∠CFE + ∠FEC = 180° - 65° = 115°，
∴∠DEB + ∠FEC = 115°，
∴∠DEF = 180° - 115° = 65°. 故选 C.

$12.[$几何模型$]$如图，$∠ABC = ∠ACB，$$AD，$$BD，$$CD$分别平分$△ABC$的外角$∠EAC、$内角$∠ABC、$外角$∠ACF.$以下结论错误的是$( )$
$A.AD//BC$
$B.∠ACB = 2∠ADB$
$C.∠ADC = 90° - ∠ABD$
$D.∠BDC = ∠BAC$
$　　　　　　　　　　　　　　　　　　　　$

答案： D [解析]
∵AD 平分△ABC 的外角∠EAC，
∴∠EAD = ∠DAC.
∵∠EAC = ∠ACB + ∠ABC，且∠ABC = ∠ACB，
∴∠EAD = ∠ABC，
∴AD//BC，故 A 正确. 由 AD//BC，
∴∠ADB = ∠DBC.
∵BD 平分∠ABC，
∴∠ABD = ∠DBC，
∴∠ABC = 2∠ADB.
∵∠ABC = ∠ACB，
∴∠ACB = 2∠ADB，故 B 正确. 在△ADC 中，∠ADC + ∠CAD + ∠ACD = 180°.
∵CD 平分△ABC 的外角∠ACF，
∴∠ACD = ∠DCF.
∵AD//BC，
∴∠ADC = ∠DCF，∠ADB = ∠DBC，∠CAD = ∠ACB，
∴∠ACD = ∠ADC，∠CAD = ∠ACB = ∠ABC = 2∠ABD，
∴∠ADC + ∠CAD + ∠ACD = ∠ADC + 2∠ABD + ∠ADC = 2∠ADC + 2∠ABD = 180°，
∴∠ADC + ∠ABD = 90°，
∴∠ADC = 90° - ∠ABD，故 C 正确.
∵∠BAC + ∠ABC = ∠ACF，
∴$\frac{1}{2}$∠BAC + $\frac{1}{2}$∠ABC = $\frac{1}{2}$∠ACF.
∵∠BDC + ∠DBC = $\frac{1}{2}$∠ACF，
∴$\frac{1}{2}$∠BAC + $\frac{1}{2}$∠ABC = ∠BDC + ∠DBC.
∵∠DBC = $\frac{1}{2}$∠ABC，
∴∠BDC = $\frac{1}{2}$∠BAC，
∴D 错误. 故选 D.