《2025年海淀单元测试AB卷七年级数学下册鲁教版》

14. [推理能力]甲、乙、丙三位同学中有一位做了一件好事，老师问他们是谁做的，他们这样回答：
甲说：“我没有做这件事，乙也没有做这件事.”
乙说：“我没有做这件事，丙也没有做这件事.”
丙说：“我没有做这件事，也不知道谁做了这件事.”
他们三人的回答中都有一句真话，一句假话. 根据这些条件判断，做好事的是_______.

答案： 乙 [解析]当甲说的没有做这件事错误，则乙也没有做这件事就正确，即甲做了好事；则乙说的没有做这件事就正确，故丙也没有做这件事就错误，即丙做了好事，与甲做了好事冲突.当甲说的没有做这件事正确，则乙也没有做这件事就错误；则乙说的没有做这件事就错误，故丙也没有做这件事就正确；则丙说没有做这件事正确，也不知道谁做了这件事错误，综上所述：做好事的是乙.故答案为乙.

$15.($淄博张店期末$)$如图，在$△ABC$中，将边$BC$沿虚线翻折，若$∠1+∠2 = 110°，$则$∠A$的度数是$_______°.$

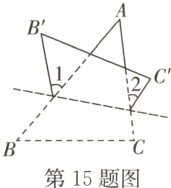
答案：
55 [解析]如图，延长B'E，C'F交于点D.由折叠可得，∠B=∠B'，∠C=∠C'，
∴∠A=∠D.又
∵∠1+∠2=110°，
∴∠AED+∠AFD=360°-110°=250°，
∴在四边形AEDF中，∠A=$\frac{1}{2}$×(360°-250°)=55°.

$16.($易错题$)($淄博博兴期末$)$如图，$AB⊥AC，$$CD，$$BE$是$△ABC$的角平分线，$AG//BC，$下列结论：$①∠BAG = 2∠ABF；$$②BA$平分$∠CBG；$$③∠ABG = ∠ACB；$$④∠CFB = 135°. $其中正确的结论是$___________.($填序号$)$

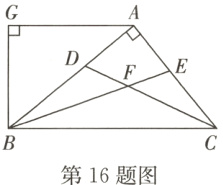
答案： ①③④ [解析]
∵BE平分∠ABC，
∴∠ABF=∠CBF=$\frac{1}{2}$∠ABC.
∵AG//BC，
∴∠BAG=∠ABC，
∴∠BAG=2∠ABF，故①正确.BA不一定平分∠CBG，故②错误.
∵BG⊥AG，
∴∠GAB+∠ABG=90°，
∴∠GBA+∠ABC=90°.
∵AB⊥AC，
∴∠ABC+∠ACB=90°，
∴∠ABG=∠ACB，故③正确.
∵CD，BE分别是△ABC的角平分线，
∴∠EBC=$\frac{1}{2}$∠ABC，∠DCB=$\frac{1}{2}$∠ACB.
∵∠ABC+∠ACB=90°，
∴∠CFB=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-45°=135°，故④正确.故答案为①③④.

$17.(10$分$)$如图，已知$AD⊥BC，$垂足为点$D，$$EF⊥BC，$垂足为点$F，$若$∠1 = ∠2，$则$GD$与$AC$平行吗$？$为什么$？$

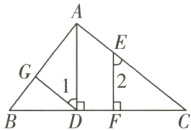
答案： 解：GD//AC，理由如下：
∵AD⊥BC，EF⊥BC，
∴AD//EF，
∴∠DAC=∠2.又
∵∠1=∠2，
∴∠DAC=∠1，
∴GD//AC.