《2025年海淀单元测试AB卷七年级数学下册鲁教版》

6.(多选)下列三角形中，是等边三角形的是( )
A. 有一个角为60°的等腰三角形
B. 有两个外角相等的等腰三角形
C. 三个外角都相等的三角形
D. 腰上的高也是这条腰上的中线的等腰三角形

答案： ACD

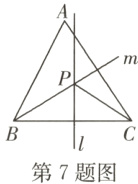
$7. $如图，在锐角三角形$ABC$中，直线$l$为$BC$的中垂线，射线$m$为$∠ABC$的平分线，$l$与$m$相交于点$P. $若$∠A=60°，$$∠ACP=24°，$则$∠ABP$的度数为$( )$
$A. 24° B. 30° C. 32° D. 36°$
$　　$

答案： C [解析]
∵射线m为∠ABC的平分线，
∴∠ABP = ∠CBP.
∵直线l为BC的中垂线，
∴BP = CP，
∴∠CBP = ∠BCP，
∴∠ABP = ∠CBP = ∠BCP. 在△ABC中，3∠ABP + ∠A + ∠ACP = 180°，即3∠ABP + 60° + 24° = 180°，解得∠ABP = 32°. 故选C.

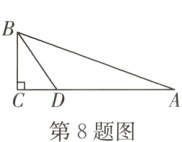
8.(张家界中考)如图，在△ABC中，∠C=90°，AC=8，DC=$\frac{1}{3}$AD，BD平分∠ABC，则点D到AB的距离等于( )
A. 4 B. 3 C. 2 D. 1
　　　　　

答案：
C [解析]如图，过点D作DE⊥AB于点E.
∵AC = 8，DC = $\frac{1}{3}$AD，
∴CD = 8×$\frac{1}{1 + 3}$ = 2.
∵∠C = 90°，BD平分∠ABC，
∴DE = CD = 2，即点D到AB的距离等于2. 故选C.

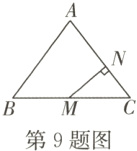
9. 如图，在△ABC中，AB=AC=5，BC=6，点M为BC的中点，MN⊥AC于点N，则MN等于( )
A. $\frac{6}{5}$ B. $\frac{9}{5}$ C. $\frac{12}{5}$ D. $\frac{16}{5}$
　　　　　

答案： C [解析]连接AM.
∵AB = AC，点M为BC的中点，
∴AM⊥CM（三线合一），BM = CM.
∵AB = AC = 5，BC = 6，
∴BM = CM = 3. 在Rt△ABM中，AB = 5，BM = 3，
∴根据勾股定理，得AM = $\sqrt{AB^{2}-BM^{2}}$ = $\sqrt{5^{2}-3^{2}}$ = 4. 又$S_{\triangle AMC}$ = $\frac{1}{2}$MN·AC = $\frac{1}{2}$AM·CM，
∴MN = $\frac{AM·CM}{AC}$ = $\frac{12}{5}$. 故选C.
★速解技巧
牢记结论：直角三角形斜边上的高等于两条直角边的乘积除以斜边.

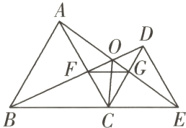
$10.［$推理能力$］$如图所示，已知$△ABC$和$△DCE$均是等边三角形，点$B，$$C，$$E$在同一条直线上，$AE$与$BD$交于点$O，$$AE$与$CD$交于点$G，$$AC$与$BD$交于点$F，$连接$OC，$$FG，$则下列结论：$①AE=BD；$$②AG=BF；$$③FG//BE；$$④∠BOC=∠EOC. $其中正确的结论有$( )$
$A. 1$个$ B. 2$个$ C. 3$个$ D. 4$个
$　　　　　　　　　　　　　　　　　　$

答案：
$D [$解析$]$
∵$△ABC$和$△DCE$均是等边三角形，
∴$BC = AC，$$CD = CE，$$∠ACB = ∠ECD = 60°，$
∴$∠ACB + ∠ACD = ∠ACD + ∠ECD，$$∠ACD = 60°，$
∴$△BCD≌△ACE（SAS），$
∴$AE = BD，$
∴$①$正确；由$①$得$∠CBD = ∠CAE. $
∵$∠BCA = ∠ACG = 60°，$$BC = AC，$
∴$△BCF≌△ACG（ASA），$
∴$AG = BF，$
∴$②$正确；同理：$△DFC≌△EGC（ASA），$
∴$CF = CG，$
∴$△CFG$是等边三角形，
∴$∠CFG = ∠FCB = 60°，$
∴$FG//BE，$
∴$③$正确；如图，过点$C$作$CM⊥AE$于点$M，$$CN⊥BD$于点$N. $
∵$△BCD≌△ACE，$
∴$∠BDC = ∠AEC. $
∵$CD = CE，$$∠CND = ∠CME = 90°，$
∴$△CDN≌△CEM（AAS），$
∴$CM = CN. $
∵$CM⊥AE，$$CN⊥BD，$
∴$Rt△OCN≌Rt△OCM（HL），$
∴$∠BOC = ∠EOC，$
∴$④$正确$. $故正确的结论有$4$个，故选$D.$

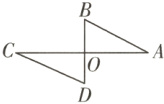
$11.($威海文登期末$)$如图，已知$AC⊥BD，$垂足为$O，$$AO=CO，$$AB=CD，$则可得到$△AOB≌△COD，$理由是定理$________.$
$　　　　　　　　　　$

答案： HL

12. 写出命题“如果两个三角形全等，那么这两个三角形的周长相等”的逆命题：______________________________，该逆命题是________命题.(填“真”或“假”)

答案： 如果两个三角形的周长相等，那么这两个三角形全等 假