《2025年海淀单元测试AB卷七年级数学下册鲁教版》

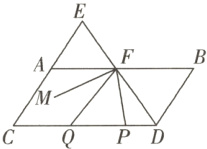
12.(泰安新泰期末)如图，点$E$在$CA$的延长线上，$DE$，$AB$交于点$F$，且$\angle BDE = \angle AEF$，$\angle B = \angle C$，$\angle EFA$比$\angle FDC$的余角小$10^{\circ}$，$P$为线段$DC$上一动点，$Q$为$PC$上一点，且满足$\angle FQP = \angle QFP$，$FM$为$\angle EFP$的平分线.下列结论不正确的是(　　　)

A. $AB// CD$
B. $FQ$平分$\angle AFP$
C. $\angle B + \angle E = 120^{\circ}$
D. $\angle QFM = 20^{\circ}$

答案： C [解析]
∵∠BDE = ∠AEF，
∴CE//BD，
∴∠B = ∠EAF.
∵∠B = ∠C，
∴∠EAF = ∠C，
∴AB//CD，
∴选项A正确.
∵AB//CD，
∴∠AFQ = ∠FQP.
∵∠FQP = ∠QFP，
∴∠AFQ = ∠QFP，
∴FQ平分∠AFP，
∴选项B正确.
∵AB//CD，
∴∠EFA = ∠FDC.
∵∠EFA比∠FDC的余角小10°，
∴∠EFA = 40°.
∵∠B = ∠EAF，∠EAF + ∠E + ∠EFA = 180°，
∴∠B + ∠E = 180° - ∠EFA = 140°，
∴选项C不正确.
∵FM为∠EFP的平分线，
∴∠MFP = $\frac{1}{2}$∠EFP = $\frac{1}{2}$∠EFA + $\frac{1}{2}$∠AFP.
∵∠AFQ = ∠QFP，
∴∠QFP = $\frac{1}{2}$∠AFP，
∴∠QFM = ∠MFP - ∠QFP = $\frac{1}{2}$∠EFA = 20°，
∴选项D正确. 故选C.

13.(东营利津月考)如图是教室门上用平行线装饰的金属条，若$\angle1 = 58^{\circ}$，则$\angle2 =$_______.
　　　

答案： 58°

14. 若在$\triangle ABC$中，$2(\angle A + \angle C) = 3\angle B$，则$\angle B$的外角度数是_______.

答案： 108°

15. 已知关于$x$，$y$的二元一次方程组$\begin{cases}2x + 3y = k\\x + 2y = -1\end{cases}$的解互为相反数，则$k$的值是_______.

答案： -1

16.(易错题)(烟台龙口期中)小红和小明做游戏，他们先在地上画了半径分别为2m和3m的同心圆(如图),然后蒙上眼睛在一定距离外向圈内掷小石子，掷中阴影部分小红胜，否则小明胜，未掷入圈内的不算，_______获胜的可能性大.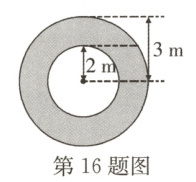

答案： 小红 [解析]S大圆 = 9π m²，S小圆 = 4π m²，S圆环 = 9π - 4π = 5π(m²). 由于小圆面积＜圆环面积，获胜可能性大的是小红.

17. 若直线$y = ax + 7$经过一次函数$y = 4 - 3x$和$y = 2x - 1$的交点，则$a$的值是_______.

答案： -6

18.(淄博临淄期末)如图,在$\triangle ABC$中，$\angle BAC ＞ \angle C$，$BD$，$BE$分别是$\triangle ABC$的高和角平分线，点$G$在$BD$的延长线上，$GH\perp BC$于点$H$，交射线$BE$于点$M$，交$AC$于点$F$，下列结论：①$\angle ABD = \angle C$；②$\angle BEA = \angle ABE + \angle ABD$；③$\angle AFG = \angle ABE + \angle DBE$；④$\angle G + \frac{1}{2}\angle A = \angle BMH + \frac{1}{2}\angle C$. 其中正确的是_______.(填序号)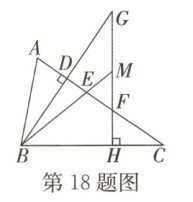

答案： ③④ [解析]
∵GH⊥BC，BG⊥AC，
∴∠BDC = ∠BHG = 90°，
∴∠G + ∠GBH = ∠DBC + ∠C = 90°，
∴∠G = ∠C. 若∠ABD = ∠C，则∠ABD = ∠G，则有AB//GH，而已知条件并不能对此证明，因此①错误.
∵BE平分∠ABC，
∴∠ABE = ∠EBC.
∵∠BEA = ∠EBC + ∠C，
∴∠BEA = ∠ABE + ∠C，由于①不能证明∠C = ∠ABD，故②错误. ∠AFG = ∠HFC(对顶角相等).
∵GH⊥BC，BG⊥AC，
∴∠HFC = ∠BDC = 90°，
∴∠HFC + ∠C = 90°，∠DBC + ∠C = 90°，
∴∠HFC = ∠DBC = ∠DBE + ∠EBC. 又
∵BE平分∠ABC，
∴∠ABE = ∠EBC，
∴∠HFC = ∠DBC = ∠DBE + ∠EBC = ∠ABE + ∠DBE，因此，∠AFG = ∠HFC = ∠ABE + ∠DBE，故③正确.
∵BG⊥AC，
∴∠ADB = ∠BDC = 90°，
∴∠A + ∠ABD = ∠DBC + ∠C = 90°，
∴∠A - ∠C = ∠DBC - ∠ABD = ∠DBE + ∠EBC - ∠ABD. 又
∵BE平分∠ABC，
∴∠ABE = ∠EBC，
∴∠A - ∠C = ∠DBE + ∠ABE - ∠ABD = 2∠DBE. 又
∵∠BMH = ∠DBE + ∠G，
∴∠BMH = $\frac{1}{2}$(∠A - ∠C) + ∠G，即∠G + $\frac{1}{2}$∠A = ∠BMH + $\frac{1}{2}$∠C，故④正确，故答案为③④.