2025年海淀单元测试AB卷七年级数学下册鲁教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年海淀单元测试AB卷七年级数学下册鲁教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
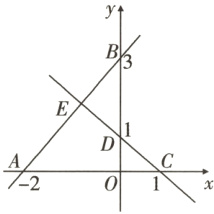
22.(10分)(威海乳山期中)如图,直线$AB$分别与$x$轴、$y$轴交于点$A(-2,0)$,$B(0,3)$. 直线$CD$分别与$x$轴、$y$轴交于点$C(1,0)$,$D(0,1)$,与直线$AB$交于点$E$. 求四边形$AODE$的面积.

答案:
解:设直线AB的函数表达式为y = kx + b,将点A(-2,0),B(0,3)代入,得$\begin{cases}0 = -2k + b\\3 = b\end{cases}$,解得$\begin{cases}k = \frac{3}{2}\\b = 3\end{cases}$,
∴直线AB的函数表达式为y = $\frac{3}{2}$x + 3,设直线CD的函数表达式为y = mx + n,将点C(1,0),D(0,1)代入,得$\begin{cases}0 = m + n\\1 = n\end{cases}$,解得$\begin{cases}m = -1\\n = 1\end{cases}$,
∴直线CD的函数表达式为y = -x + 1,联立得$\begin{cases}y = \frac{3}{2}x + 3\\y = -x + 1\end{cases}$,解得$\begin{cases}x = -\frac{4}{5}\\y = \frac{9}{5}\end{cases}$,
∴E(-$\frac{4}{5}$,$\frac{9}{5}$),
∴S四边形AODE = S△ACE - S△OCD = $\frac{1}{2}$×(1 + 2)×$\frac{9}{5}$ - $\frac{1}{2}$×1×1 = $\frac{11}{5}$.
∴直线AB的函数表达式为y = $\frac{3}{2}$x + 3,设直线CD的函数表达式为y = mx + n,将点C(1,0),D(0,1)代入,得$\begin{cases}0 = m + n\\1 = n\end{cases}$,解得$\begin{cases}m = -1\\n = 1\end{cases}$,
∴直线CD的函数表达式为y = -x + 1,联立得$\begin{cases}y = \frac{3}{2}x + 3\\y = -x + 1\end{cases}$,解得$\begin{cases}x = -\frac{4}{5}\\y = \frac{9}{5}\end{cases}$,
∴E(-$\frac{4}{5}$,$\frac{9}{5}$),
∴S四边形AODE = S△ACE - S△OCD = $\frac{1}{2}$×(1 + 2)×$\frac{9}{5}$ - $\frac{1}{2}$×1×1 = $\frac{11}{5}$.
23.(12分)[模型观念]某型号动车由一节车头和若干节车厢组成,每节车厢的长度都相等. 已知该型号动车挂8节车厢以38米/秒的速度通过某观测点用时6秒,挂12节车厢以41米/秒的速度通过该观测点用时8秒.
(1)车头及每节车厢的长度分别是多少米?
(2)小明乘坐该型号动车匀速通过某隧道时,如果车头进隧道5秒后他也进入了隧道,此时车内屏幕显示速度为180千米/时,他乘坐的是几号车厢?
(1)车头及每节车厢的长度分别是多少米?
(2)小明乘坐该型号动车匀速通过某隧道时,如果车头进隧道5秒后他也进入了隧道,此时车内屏幕显示速度为180千米/时,他乘坐的是几号车厢?
答案:
解:
(1)设车头的长度是x米,每节车厢的长度是y米. 根据题意,得$\begin{cases}x + 8y = 38×6\\x + 12y = 41×8\end{cases}$,解得$\begin{cases}x = 28\\y = 25\end{cases}$. 答:车头的长度是28米,每节车厢的长度是25米.
(2)180千米/时 = 50米/秒,(50×5 - 28)÷25 = 8.88. 答:小明乘坐的是9号车厢.
(1)设车头的长度是x米,每节车厢的长度是y米. 根据题意,得$\begin{cases}x + 8y = 38×6\\x + 12y = 41×8\end{cases}$,解得$\begin{cases}x = 28\\y = 25\end{cases}$. 答:车头的长度是28米,每节车厢的长度是25米.
(2)180千米/时 = 50米/秒,(50×5 - 28)÷25 = 8.88. 答:小明乘坐的是9号车厢.
24.(14分)[新动向.探究性试题](烟台福山期中)已知$AB// CD$,直线$EF$分别交$AB$,$CD$于点$E$,$F$,直线$GH$分别交$AB$,$CD$于点$G$,$H$.
(1)如图①,若$\angle BGH = 80^{\circ}$,$\angle BEF = 120^{\circ}$,$EM$平分$\angle AEF$,$HM$平分$\angle GHC$,求$\angle EMH$的度数.
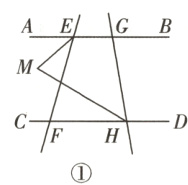
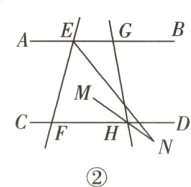
(2)如图②,$HM$平分$\angle GHC$,$EN$平分$\angle BEF$交$MH$的延长线于点$N$,探究$\angle MNE$,$\angle BGH$,$\angle BEF$之间的数量关系,并说明理由.
(1)如图①,若$\angle BGH = 80^{\circ}$,$\angle BEF = 120^{\circ}$,$EM$平分$\angle AEF$,$HM$平分$\angle GHC$,求$\angle EMH$的度数.

(2)如图②,$HM$平分$\angle GHC$,$EN$平分$\angle BEF$交$MH$的延长线于点$N$,探究$\angle MNE$,$\angle BGH$,$\angle BEF$之间的数量关系,并说明理由.

答案:
解:
(1)过点M作MN//AB. 如图①.
∵AB//CD,MN//AB,
∴MN//CD,∠BGH = ∠GHC = 80°.
∵HM平分∠GHC,
∴∠MHC = $\frac{1}{2}$∠GHC = 40°.
∵∠BEF = 120°,
∴∠AEF = 60°.
∵EM平分∠AEF,
∴∠AEM = $\frac{1}{2}$∠AEF = 30°.
∵MN//AB//CD,
∴∠EMN = ∠AEM = 30°,∠HMN = ∠MHC = 40°,
∴∠EMH = ∠EMN + ∠HMN = 30° + 40° = 70°.
(2)∠MNE = $\frac{1}{2}$∠BEF - $\frac{1}{2}$∠BGH. 理由:过点N作NK//CD,如图②.
∵AB//CD,
∴NK//AB,
∴∠ENK = ∠BEN.
∵EN平分∠BEF,
∴∠ENK = ∠BEN = $\frac{1}{2}$∠BEF.
∵NK//CD,
∴∠MHC = ∠MNK.
∵HM平分∠GHC,
∴∠MHC = $\frac{1}{2}$∠GHC. 又
∵AB//CD,
∴∠BGH = ∠GHC,
∴∠MNK = $\frac{1}{2}$∠BGH,
∴∠MNE = ∠ENK - ∠MNK,
∴∠MNE = $\frac{1}{2}$∠BEF - $\frac{1}{2}$∠BGH.

解:
(1)过点M作MN//AB. 如图①.
∵AB//CD,MN//AB,
∴MN//CD,∠BGH = ∠GHC = 80°.
∵HM平分∠GHC,
∴∠MHC = $\frac{1}{2}$∠GHC = 40°.
∵∠BEF = 120°,
∴∠AEF = 60°.
∵EM平分∠AEF,
∴∠AEM = $\frac{1}{2}$∠AEF = 30°.
∵MN//AB//CD,
∴∠EMN = ∠AEM = 30°,∠HMN = ∠MHC = 40°,
∴∠EMH = ∠EMN + ∠HMN = 30° + 40° = 70°.
(2)∠MNE = $\frac{1}{2}$∠BEF - $\frac{1}{2}$∠BGH. 理由:过点N作NK//CD,如图②.
∵AB//CD,
∴NK//AB,
∴∠ENK = ∠BEN.
∵EN平分∠BEF,
∴∠ENK = ∠BEN = $\frac{1}{2}$∠BEF.
∵NK//CD,
∴∠MHC = ∠MNK.
∵HM平分∠GHC,
∴∠MHC = $\frac{1}{2}$∠GHC. 又
∵AB//CD,
∴∠BGH = ∠GHC,
∴∠MNK = $\frac{1}{2}$∠BGH,
∴∠MNE = ∠ENK - ∠MNK,
∴∠MNE = $\frac{1}{2}$∠BEF - $\frac{1}{2}$∠BGH.

查看更多完整答案,请扫码查看


