《2025年海淀单元测试AB卷七年级数学下册鲁教版》

13.[分类讨论思想](武威中考)定义：等腰三角形的顶角与其中一个底角的度数的比值k称为这个等腰三角形的“特征值”. 若在等腰三角形ABC中，∠A=80°，则它的特征值k=_______.

答案： $\frac{8}{5}$或$\frac{1}{4}$ [解析]①当∠A 为顶角时，等腰三角形两底角的度数为$\frac{180° - 80°}{2}$ = 50°，
∴特征值 k = $\frac{80°}{50°}$ = $\frac{8}{5}$；②当∠A 为底角时，顶角的度数为 180° - 80° - 80° = 20°，
∴特征值 k = $\frac{20°}{80°}$ = $\frac{1}{4}$. 综上所述，特征值 k 为$\frac{8}{5}$或$\frac{1}{4}$. ★易错警示 解答本题时，一定要分类讨论，∠A 可能为顶角，也可能为底角，两者缺一不可. 

$14. $如图，$OP$平分$∠MON，$$PE⊥OM$于点$E，$$PF⊥ON$于点$F，$$OA=OB，$则图中有$_______$对全等三角形$.$

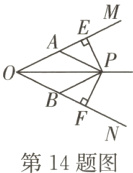
答案： 3

$15.[$几何模型$]$如图，在四边形$ABCD$中，$AB=AD，$$∠BAD=∠BCD=90°，$连接$AC. $若$AC=6，$则四边形$ABCD$的面积为$_______.$

答案：
18 [解析]如图，延长 CB 到点 E，使 BE = DC，连接 AE，
∴∠ABE + ∠ABC = 180°.
∵∠BAD = ∠BCD = 90°，
∴∠D + ∠ABC = 180°，
∴∠ABE = ∠D.
∵AB = AD，BE = DC，
∴△ABE≌△ADC（SAS），
∴∠EAB = ∠DAC，AE = AC，△ABE 与△ADC 的面积相等，
∴∠CAB + ∠EAB = ∠BAC + ∠DAC = 90°，即∠EAC = 90°，
∴△EAC 是等腰直角三角形，
∴四边形 ABCD 的面积 = △EAC 的面积 = $\frac{1}{2}$×6² = 18. 

$16.[$推理能力$]$如图，已知$∠AOB=α，$在射线$OA，$$OB$上分别取点$A1，$$B1，$使$OA1=OB1，$连接$A1B1，$在$B1A1，$$B1B$上分别取点$A2，$$B2，$使$B1B2=B1A2，$连接$A2B2……$按此规律下去，记$∠A2B1B2=θ1，$$∠A3B2B3=θ2，$$…，$$An+1BnBn+1=θn，$则$θ1=__________，$$θn=__________.$

答案：
∴∠A₁B₁O = $\frac{1}{2}$(180° - α)，
∴θ₁ = 180° - $\frac{1}{2}$(180° - α) = $\frac{180° + α}{2}$.
∵A₂B₁ = B₁B₂，
∴∠A₂B₂B₁ = $\frac{1}{2}$(180° - $\frac{180° + α}{2}$) = $\frac{180° - α}{4}$，
∴θ₂ = 180° - ∠A₂B₂B₁ = 180° - $\frac{180° - α}{4}$ = $\frac{3×180° + α}{4}$，同理可得θ₃ = $\frac{7×180° + α}{8}$，…，
∴θₙ = $\frac{(2ⁿ - 1)·180° + α}{2ⁿ}$.

$17.(10$分$)$如图，在$△ABC$中，$AB=CB，$$∠ABC=90°，$$F$为$AB$延长线上一点，点$E$在$BC$上，且$AE=CF.$
$(1)$求证：$Rt△ABE≌Rt△CBF.$
$(2)$若$∠CAE=30°，$求$∠ACF$的度数$.$

答案：
(1)证明：
∵∠ABC = 90°，
∴∠CBF =∠ABE = 90°. 在Rt△ABE和Rt△CBF中，
∵AE = CF，AB = CB，
∴Rt△ABE≌Rt△CBF(HL).
(2)解：
∵AB = BC，∠ABC = 90°，
∴∠CAB =∠ACB = 45°.
∴∠BAE =∠CAB - ∠CAE = 45° - 30° = 15°. 由
(1)知Rt△ABE≌Rt△CBF，
∴∠BCF =∠BAE = 15°.
∴∠ACF =∠BCF +∠ACB = 15° + 45° = 60°.