《2025年海淀单元测试AB卷七年级数学下册鲁教版》

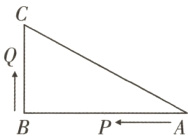
$21.(12$分$)($东营河口期末$)$如图，在$△ABC$中，$∠B=90°，$$AB=16 cm，$$BC=12 cm，$$P，$$Q$是$△ABC$边上的两个动点，其中点$P$从点$A$开始沿$A→B$方向运动，且速度为每秒$1 cm，$点$Q$从点$B$开始沿$B→C→A$方向运动，且速度为每秒$2 cm，$它们同时出发，同时停止$.$
$(1)P，$$Q$出发$5$秒后，求$PQ$的长$.$
$(2)$当点$Q$在边$CA$上运动时，出发几秒时，$△CQB$能形成直角三角形$？$

答案： 解：
(1)由题意可得BQ = 2×5 = 10(cm)，BP = AB - AP = 16 - 1×5 = 11(cm).
∵∠B = 90°，
∴PQ = $\sqrt{BP² + BQ²}$ = $\sqrt{11² + 10²}$ = $\sqrt{221}$(cm)，即PQ的长为$\sqrt{221}$cm.
(2)当BQ⊥AC时，∠BQC = 90°.
∵∠ABC = 90°，AB = 16 cm，BC = 12 cm，
∴AC = $\sqrt{AB² + BC²}$ = $\sqrt{16² + 12²}$ = 20(cm).
∵$\frac{AB·BC}{2}$ = $\frac{AC·BQ}{2}$，
∴$\frac{16×12}{2}$ = $\frac{20BQ}{2}$，解得BQ = $\frac{48}{5}$cm，
∴CQ = $\sqrt{BC² - BQ²}$ = $\sqrt{12² - (\frac{48}{5})²}$ = $\frac{36}{5}$(cm)，
∴当△CQB是直角三角形时，经过的时间为(12 + $\frac{36}{5}$)÷2 = 9.6(秒)；当∠CBQ = 90°时，点Q运动到点A，此时运动的时间为(12 + 20)÷2 = 16(秒). 综上，当点Q在边CA上运动时，出发9.6秒或16秒时，△CQB能形成直角三角形.

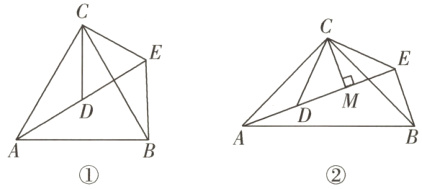
$22.(14$分$)[$新动向$·$探究性试题$](1)【$问题发现$】$如图$①，$$△ACB$和$△DCE$均为等边三角形，点$A，$$D，$$E$在同一直线上，连接$BE. $填空：
$①∠AEB$的度数为$_______.$
$②$线段$AD，$$BE$之间的数量关系为$_______.$
$(2)【$拓展探究$】$如图$②，$$△ACB$和$△DCE$均为等腰直角三角形，$∠ACB=∠DCE=90°，$点$A，$$D，$$E$在同一直线上，$CM$为$△DCE$中$DE$边上的高，连接$BE. $请判断$∠AEB$的度数及线段$CM，$$AE，$$BE$之间的数量关系，并说明理由$.$

答案： 解：
(1)①60° ②AD = BE
(2)∠AEB = 90°，AE = 2CM + BE. 理由：
∵△ACB和△DCE均为等腰直角三角形，∠ACB =∠DCE = 90°，
∴AC = BC，CD = CE，∠CDE =∠CED = 45°，∠ACB - ∠DCB =∠DCE - ∠DCB，即∠ACD = ∠BCE，
∴△ACD≌△BCE，
∴AD = BE，∠BEC =∠ADC = 135°，
∴∠AEB =∠BEC - ∠CED = 135° - 45° = 90°. 在等腰直角三角形DCE中，CM为斜边DE上的高，
∴CM = DM = ME，
∴DE = 2CM，
∴AE = DE + AD = 2CM + BE.

附加题$（10$分$）$
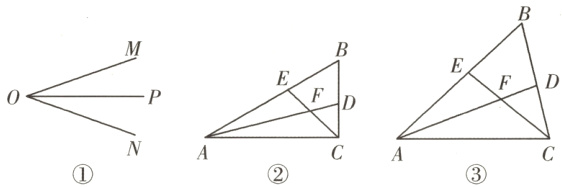
$23.[$推理能力$]（1）$如图$①，$$OP$是$∠MON$的平分线，请你利用该图形画一对以$OP$所在直线为对称轴的全等三角形$. $请你参考这个作全等三角形的方法，解答下列问题$.$
$（2）$如图$②，$在$△ABC$中，$∠ACB$是直角，$∠B=60°，$$AD，$$CE$分别是$∠BAC，$$∠BCA$的平分线，$AD，$$CE$相交于点$F，$请你判断并写出$FE$与$FD$之间的数量关系$.（$不需写证明过程$）$
$（3）$如图$③，$在$△ABC$中，如果$∠ACB$不是直角，而$（2）$中的其他条件不变，请问你在$（2）$中所得结论是否仍然成立$. $若成立，请证明；若不成立，请说明理由$.$

答案：
解：$(1)$如图$①$所示$. ($答案不唯一$) (2)FE$与$FD$之间的数量关系为$FE = FD. (3)(2)$中的结论$FE = FD$仍然成立$. $证明如下：如图$②，$过点$F$分别作$FG⊥AB$于点$G，$$FH⊥BC$于点$H，$
∴$∠EGF =∠DHF = 90°. $
∵$∠B = 60°，$且$AD，$$CE$分别是$∠BAC，$$∠BCA$的平分线，
∴$∠2 +∠3 = 60°，$$∠GEF =∠2 +∠3 +∠1 = 60° +∠1. $又
∵点$F$是角平分线的交点，
∴$FG = FH. $
∵$∠HDF =∠B +∠1 = 60° +∠1，$
∴$∠GEF = ∠HDF，$
∴$△EGF≌△DHF(AAS)，$
∴$FE = FD.$