《2025年海淀单元测试AB卷七年级数学下册鲁教版》

$11. $如图是由大小完全相同的正六边形组成的图形，小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色，则上方的正六边形涂红色的概率是$_______.$
$ $

答案： $\frac{1}{3}$

12. (襄阳中考)中国象棋文化历史久远. 在图中所示的部分棋盘中，“馬”的位置在“———”(图中虚线)的下方，“馬”移动一次能够到达的所有位置已用“●”标记，则“馬”随机移动一次，到达的位置在“———”上方的概率是_______.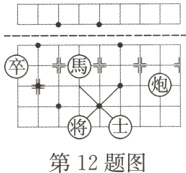

答案： $\frac{1}{4}$

$13. [$数据观念$]($金华中考$)$下表为某中学统计的七年级$500$名学生体重达标情况$($单位：人$)，$在该年级随机抽取一名学生，该生体重为$“$标准$”$的概率是$_______.$

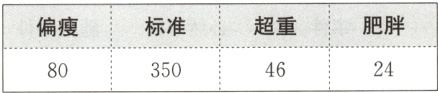
答案： $\frac{7}{10}$

$14. $在猜一商品价格的游戏中，参与者事先不知道该商品的价格，主持人要求他从图中的四张卡片中任意拿走一张，使剩下的卡片从左到右连成一个三位数，该数就是他猜的价格$. $若商品的价格是$360$元，那么他一次就能猜中的概率是$_______.$

答案： $\frac{1}{4}$

$15. ($易错题$)$已知一小球在如图所示正方形区域内滚动，正方形$ABCD$的边长为$3，$$E，$$F，$$G，$$H$分别为各边上的点，且$AE = BF = CG = DH = 1，$则小球停止后正好落在阴影区域的概率是$_______.$

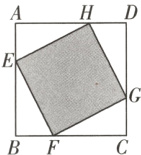
答案： $\frac{5}{9}$ [解析]根据正方形的四边相等，四个角都是直角，且$AE = BF = CG = DH$，可证$\triangle AEH\cong\triangle BFE\cong\triangle CGF\cong\triangle DHG$.$\because AE = BF = CG = DH = 1$，且正方形的边长为 3，$\therefore AH = DG = CF = BE = 2$，$\therefore EH = HG = GF = FE = \sqrt{5}$，$\therefore$正方形$EFGH$的面积为 5.$\because$正方形$ABCD$的面积为 9，$\therefore$小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.

$16. [$推理能力$]$如图，第$①$个图有$1$个黑球；第$②$个图为$3$个同样大小的球叠成的图形，最下面一层的$2$个球为黑色，其余为白色；第$③$个图为$6$个同样大小的球叠成的图形，最下面一层的$3$个球为黑色，其余为白色$……$则从第$ⓝ$个图中随机取出一个球，是黑球的概率是$_______.$

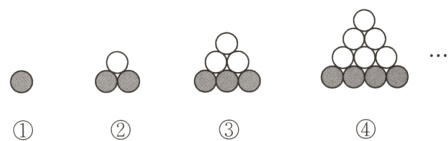
答案： $\frac{2}{n + 1}$ [解析]根据规律，第$n$个图中，黑球有$n$个，球的总数有$1 + 2 + 3 + 4 + 5 + \cdots + n = \frac{n(n + 1)}{2}$，则从第$n$个图中随机取出一个球，是黑球的概率是$\frac{n}{\frac{n(n + 1)}{2}}=\frac{2}{n + 1}$.