《2025年顶尖课课练八年级数学下册人教版》

1. 某画家用一张纸片剪拼出不一样的空洞，而两个空洞的面积是相等的，如图17.2.3−1所示，证明了勾股定理。若设图②中空白部分的面积为S₁，图③中空白部分的面积为S₂，则下列等式不正确的是(　　　)。

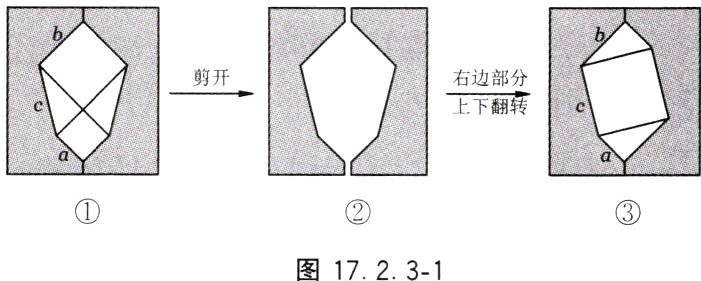
A. S₁ = a² + b² + 2ab
　B. S₂ = c² + ab
C. S₁ = S₂　　　　　　
　D. a² + b² = c²

答案： A

2. 在△ABC中，∠C = 90°，若a + b = 7，△ABC的面积等于6，则边长c = ____。

答案： 5

3. 我国汉代数学家赵爽证明勾股定理时创制了“赵爽弦图”，它是由4个全等的直角三角形和一个小正方形组成的。如图17.2.3−2，直角三角形的直角边长为a，b，斜边长为c。若b - a = 2，每个直角三角形的面积为15，则c的长为______。

答案： 8

4. 小明家承包了一个矩形鱼池，已知其面积为48m²，其对角线长为10m，为建栅栏，要计算这个矩形鱼池的周长，你能帮助小明算一算吗？

答案： 28m

5. 已知在Rt△ABC中，∠C = 90°，若a + b = 14，c = 10，求Rt△ABC的面积。
悟：求直角三角形的面积，只需求出两条直角边a，b的积，若已知a + b和a² + b²，可利用乘法公式直接求ab。

答案： 24

6. 观察下列各式，你有什么发现？
3² = 4 + 5，5² = 12 + 13，7² = 24 + 25，9² = 40 + 41，……
这到底是巧合，还是有什么规律蕴含其中呢？
(1)填空：13² = ______ + ______；
(2)请写出你发现的规律；
(3)结合勾股定理有关知识，说明你的结论的正确性。

答案：
(1)84　85
(2)略
(3)略