第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1. 在△ABC中,若∠A = 90°,∠A,∠B,∠C的对边分别为a,b,c,则下列结论中错误的是( ).
A.a² + b² = c²
B.b² + c² = a²
C.a² - b² = c²
D.a² - c² = b²
A.a² + b² = c²
B.b² + c² = a²
C.a² - b² = c²
D.a² - c² = b²
答案:
A
2.我们已经学会了运用如图17.1.1 - 1所示的图形验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数、图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( ).

A.统计思想 B.分类思想
C.数形结合思想 D.函数思想

A.统计思想 B.分类思想
C.数形结合思想 D.函数思想
答案:
C
3.如图17.1.1 - 2,大正方形的面积既可表示
为____________,又可
表示为____________
从而可得到______
________________,化
简得______________.
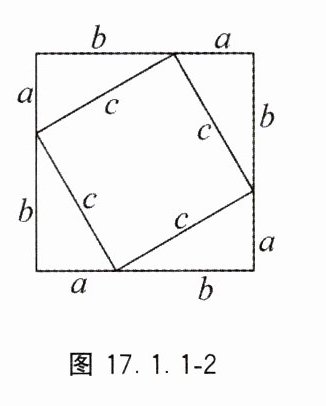
为____________,又可
表示为____________
从而可得到______
________________,化
简得______________.

答案:
略
4.图17.1.1 - 3是勾股定理的一种证明方法,你能根据图中所给的条件验证勾股定理吗?请写出推理过程.


答案:
略
查看更多完整答案,请扫码查看


