《2025年顶尖课课练八年级数学下册人教版》

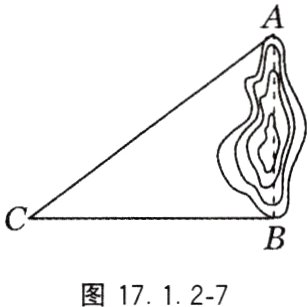
8. 如图17.1.2−7，隔湖有A，B两点，为了测得A，B两点间的距离，从与AB方向成直角的BC方向上任取一点C。若测得CA = 50m，CB = 40m，则A，B两点间的距离是______m。

答案： 30

9. 小明想知道学校旗杆的高度，他发现旗杆上的绳子垂到地面上还多1m，当他把绳子的下端拉开距旗杆底部5m后，发现绳子的末端刚好接触地面，则旗杆的高为______m。

答案： 12

10. 《九章算术》是中国传统数学的重要著作之一，奠定了中国传统数学的基本框架。其中记载了一道“折竹”问题:“今有竹高一丈，末折抵地，去本三尺。问折者高几何?”题意是:一根竹子原高1丈(1丈 = 10尺，1米 = 3尺)，中部有一处折断，竹梢触地面处离竹根3尺，示意图如图17.1.2−8所示。试问:折断处离地面多高？答:折断处离地面________尺高。

答案： 4.55

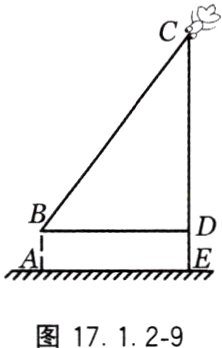
11. 某城市广场视野开阔，阻挡物少，成为不少市民放风筝的热门场所。小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度CE，他们前往广场进行了如下操作:①测得水平距离BD的长为15m；②根据手中剩余线的长度计算出风筝线BC的长为25m；③牵线放风筝的小明的身高AB为1.6m。(示意图如图17.1.2−9所示)
(1)求风筝的垂直高度CE；
(2)如果小明想让风筝沿CD方向下降12m，那么他应该往回收线多少米？

答案：
(1)21.6m
(2)8m