《2025年通城学典初中数学运算能手八年级下册苏科版》

1. 在$\square ABCD$中，$\angle A:\angle B = 7:2$，则$\angle C$的度数为_______.

答案： 140°

2. 如图，$\square ABCD$的周长为 22，$\triangle ABC$的周长为 17，则$AC$的长为_______.

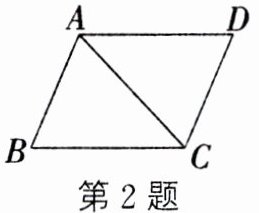
答案： 6

3. 如图，在$\square ABCD$中，$AC = AD$，$\angle D = 70^{\circ}$，$BE\perp AC$，垂足为$E$，则$\angle ABE$的度数为_______.

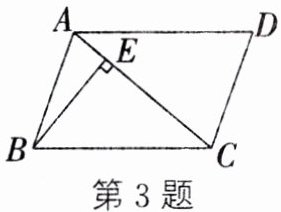
答案： 20°

4. 若$\square ABCD$的一个内角的平分线把一条边分成 4 cm 和 5 cm 的两段，则$\square ABCD$的周长为_______cm.

答案： 26或28

5. 如图，在$\square ABCD$中，$CE$平分$\angle BCD$，交$AB$于点$E$，$EA = 3$，$EB = 5$，$ED = 4$，则$EC$的长为_______.

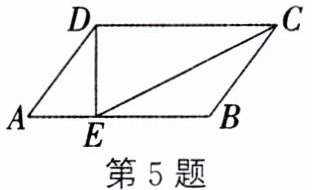
答案： $4\sqrt{5}$

6. 如图，$E$为$\square ABCD$内一点，连接$EA$、$EB$、$EC$、$ED$、$AC$. 若$\triangle BCE$的面积为 2，$\triangle ABE$的面积为 3，$\triangle CED$的面积为 10，则$\triangle ADE$的面积为_______，涂色部分的面积为_______.

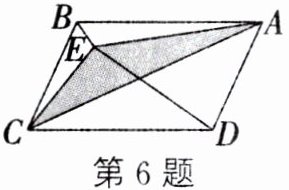
答案： 11@@8

7. 如图，在等边三角形$ABC$中，$BC = 6$cm，射线$AG// BC$，点$E$从点$A$出发，沿射线$AG$以 1 cm/s 的速度运动，同时，点$F$从点$B$出发，沿射线$BC$以 2 cm/s 的速度运动，设运动时间为$t$ s. 若以$A$、$C$、$E$、$F$为顶点的四边形是平行四边形，求$t$的值.

答案： ①当点F在点C的左侧时，根据题意，得AE = t cm，BF = 2t cm，则CF = BC - BF =（6 - 2t）cm.
∵AG//BC，
∴当AE = CF时，四边形AECF是平行四边形，即t = 6 - 2t，解得t = 2. ②当点F在点C的右侧时，根据题意，得AE = t cm，BF = 2t cm，则CF = BF - BC =（2t - 6）cm.
∵AG//BC，
∴当AE = CF时，四边形AEFC是平行四边形，即t = 2t - 6，解得t = 6. 综上所述，t的值为2或6