《2025年通城学典初中数学运算能手八年级下册苏科版》

1. 如图，在△ABC中，AB = AC，BC = 100，AD平分∠BAC，则BD = _______.

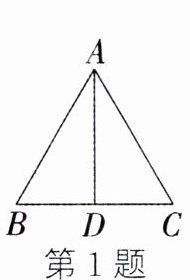
第1题 第2题 第3题

答案： 50

2. 如图，CE、AD相交于点B，∠ACB = 90°，∠A = 60°，BD = BE，则∠E的度数为________.

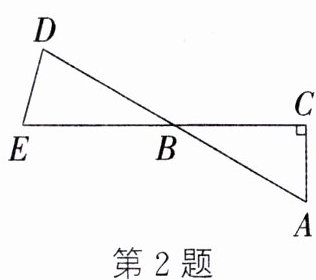
答案： 75°

3. 如图，在△ABC中，∠A = 40°，边AB的垂直平分线分别交AB、AC于点D、E，连接BE，则∠BEC的度数为_______.

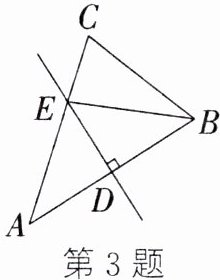
答案： 80°

4. 如图，在△ABC中，AC = AD = BD，∠B = 28°，则∠CAD的度数为_______.

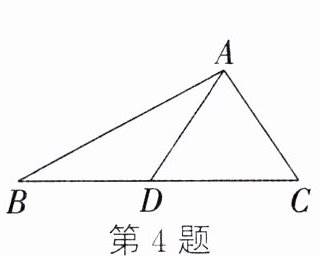
答案： 68°

5. 小宋把一张等边三角形纸片放在如图所示的两条平行线m、n上，测得∠AEG = 20°，则∠ADF的度数为_______.

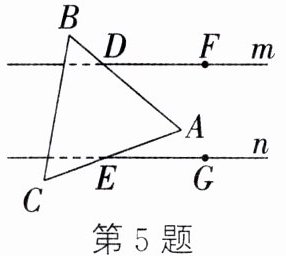
答案： 40°

6. 如图，在△ABC中，∠B = 70°，∠C = 90°，在射线BA上找一点D，使△ACD为等腰三角形，则∠ADC的度数为__________.

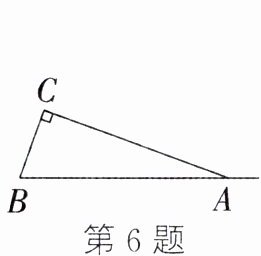
答案： 10°或80°或140°

7. 如图，等边三角形ABC的边长为12 cm，M、N两点分别从点A、B同时出发，沿△ABC的边按顺时针方向运动，点M的速度为1 cm/s，点N的速度为2 cm/s，当点N第一次到达点B时，M，N两点同时停止运动. 设运动时间为t s. 若△AMN为等腰三角形，求t的值.

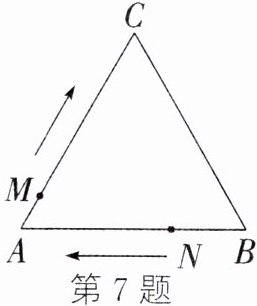
答案：

∵△ABC为等边三角形，
∴AC = BC = AB = 12 cm. 分情况讨论： ①当0≤t≤6时，点N在边AB上，点M在边AC上. 由运动知，AN=(12 - 2t)cm，AM = t cm.
∵△ABC为等边三角形，
∴∠CAB = 60°. 又
∵△AMN为等腰三角形，
∴△AMN为等边三角形.
∴AN = AM.
∴12 - 2t = t，解得t = 4. ②当6 ＜ t≤12时，点M、N都在边AC上，无法与点A构成三角形，舍去. ③当12 ＜ t≤18时，点M、N都在边BC上. 如图，当△AMN为等腰三角形时，只可能AM = AN.
∴∠AMN = ∠ANM.
∴∠AMC = ∠ANB.
∵△ABC为等边三角形，
∴∠C = ∠B，AC = AB. 在△ACM和△ABN中， $\begin{cases}\angle AMC=\angle ANB, \\\angle C=\angle B, \\AC = AB\end{cases}$
∴△ACM≌△ABN.
∴CM = BN.
∵由运动知，CM=(t - 12)cm，BN=(36 - 2t)cm，
∴t - 12 = 36 - 2t，解得t = 16. 综上所述，t的值为4或16