《2025年通城学典初中数学运算能手八年级下册苏科版》

1.（青岛中考）列车从甲地驶往乙地，行完全程所需的时间$t$（h）与行驶的平均速度$v$（km/h）之间的反比例函数的图像如图所示. 若列车要在 2.5 h 内到达，则平均速度至少需要提高到_______km/h.

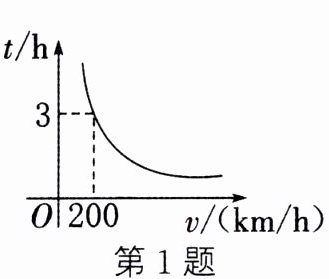
答案： 240

2. 小明要把一篇文章录入电脑，所需时间$y$（分）与录入文字的速度$x$（字/分）之间的反比例函数的图像如图所示. 若小明要在 7 分内完成录入任务，则小明录入文字的速度至少为_______字/分.

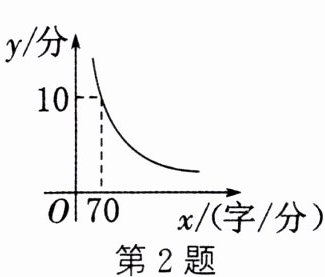
答案： 100

3. 李老师参加了某电脑公司推出的分期付款（无利息）购买电脑的活动，他购买的电脑的价格为 9 800 元，交了首付款之后每个月付款$y$元，$x$个月结清余款，$y$与$x$满足如图所示的函数关系，则李老师的首付款为_______元.

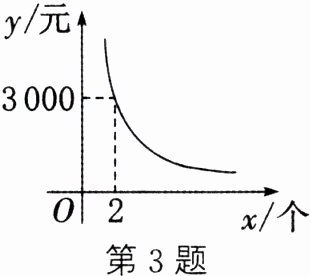
答案： 3800

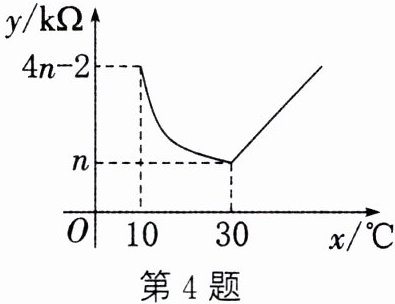
4. 电灭蚊器的电阻$y$（kΩ）随温度$x$（℃）变化的大致图像如图所示，通电后温度由 10℃上升到 30℃时，电阻与温度成反比例函数关系，且在温度达到 30℃时，电阻下降到最小值，随后电阻随温度升高而增加，温度每上升 1℃，电阻增加$\frac{1}{5}$kΩ.
（1）当$10\leq x\leq30$时，求$y$与$x$之间的函数表达式；
（2）在电灭蚊器的使用过程中，当电阻不超过 5 kΩ时，求$x$的取值范围.

答案： （1）当10≤x≤30时，设y与x之间的函数表达式为y = $\frac{m}{x}$。根据题意，得该函数图像经过点（10，4n - 2）、（30，n），
∴$\begin{cases}4n - 2=\frac{m}{10}\\n=\frac{m}{30}\end{cases}$，解得$\begin{cases}n = 2\\m = 60\end{cases}$。
∴当10≤x≤30时，y与x之间的函数表达式为y = $\frac{60}{x}$。 （2）
∵y = $\frac{60}{x}$，
∴当x = 30时，y = $\frac{60}{30}$=2。根据题意，得该函数图像经过点（30，2）。当x＞30时，设y与x之间的函数表达式为y = kx + b。
∵温度每上升1℃，电阻增加$\frac{1}{5}$kΩ，
∴该函数图像经过点（31，2$\frac{1}{5}$）。
∴$\begin{cases}30k + b = 2\\31k + b = 2\frac{1}{5}\end{cases}$，解得$\begin{cases}k=\frac{1}{5}\\b = - 4\end{cases}$。
∴当x＞30时，y与x之间的函数表达式为y = $\frac{1}{5}x - 4$。对于y = $\frac{60}{x}$，当y = 5时，x = 12；对于y = $\frac{1}{5}x - 4$，当y = 5时，x = 45。
∴在电灭蚊器的使用过程中，当电阻不超过5 kΩ时，x的取值范围是12≤x≤45。