《2025年通城学典初中数学运算能手八年级下册苏科版》

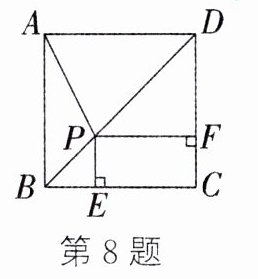
8. 如图，在正方形 ABCD 中，P 为对角线 BD 上一点，过点 P 作 PE⊥BC 于点 E，PF⊥CD 于点 F，连接 AP. 若 PE = 1，PF = 2，则 AP 的长为________.

答案： $\sqrt{5}$

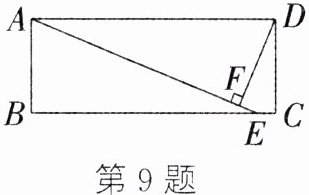
9. （22 分）如图，在矩形 ABCD 中，E 是 BC 上一点，且 AE = DA，DF⊥AE 于点 F.
（1）求证：CE = FE；
（2）若 DF = 5，CE = 1，求矩形 ABCD 的面积.

答案： （1）连接DE. 因为四边形ABCD是矩形，所以∠B = ∠C = 90°，AB = DC，DA // BC. 所以∠AEB = ∠DAF. 因为DF⊥AE，所以∠AFD = ∠B = 90°. 在△ABE和△DFA中，$\begin{cases}∠B = ∠AFD \\∠AEB = ∠DAF \\AE = DA\end{cases}$，所以△ABE≌△DFA. 所以AB = DF. 所以DF = DC. 在Rt△DCE和Rt△DFE中，$\begin{cases}DE = DE \\DC = DF\end{cases}$，所以Rt△DCE≌Rt△DFE. 所以CE = FE. （2）由（1），得DF = DC，CE = FE. 因为DF = 5，CE = 1，所以DC = 5，FE = 1. 设DA = x，则AF = AE - FE = DA - 1 = x - 1. 在Rt△DFA中，因为AF² + DF² = DA²，所以(x - 1)² + 5² = x²，解得x = 13，即DA = 13. 所以S_{矩形ABCD}= DA·DC = 65.

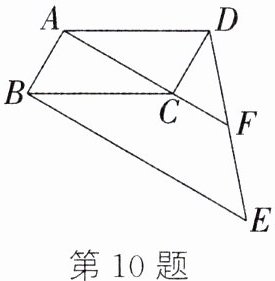
10. （22 分）如图，点 E 在□ABCD 外，连接 BE、DE，延长 AC 交 DE 于点 F，且 F 是 DE 的中点.
（1）求证：AF//BE；
（2）若 AD = 2，∠ADC = 60°，∠ACD = 90°，AC = 2CF，求 BE 的长.

答案： （1）连接BD，交AC于点O. 因为四边形ABCD是平行四边形，所以O是BD的中点. 因为F是DE的中点，所以OF是△DBE的中位线. 所以OF // BE，即AF // BE. （2）因为四边形ABCD是平行四边形，所以AC = 2OA = 2OC. 因为AC = 2CF，所以OA = OC = CF. 因为∠ADC = 60°，∠ACD = 90°，所以∠DAC = 30°. 因为AD = 2，所以易得DC = $\frac{1}{2}$AD = 1. 在Rt△ACD中，因为AC² + DC² = AD²，所以AC = $\sqrt{AD² - DC²}$ = $\sqrt{3}$. 所以OF = 2CF = AC = $\sqrt{3}$. 由（1），得OF是△DBE的中位线. 所以BE = 2OF = 2$\sqrt{3}$.