《2025年通城学典初中数学运算能手八年级下册苏科版》

1. 下列计算正确的是 （ ）
A. $\sqrt{(-3)^2}=-3$
B. $\sqrt{2}×\sqrt{5}=\sqrt{7}$
C. $\sqrt{9}÷\sqrt{3}=3$
D. $(\sqrt{2})^2=2$

答案： D

2. 下列计算正确的是 （ ）
A. $4\sqrt{3}-3\sqrt{3}=1$
B. $\sqrt{2}+\sqrt{3}=\sqrt{5}$
C. $3 + 2\sqrt{2}=5\sqrt{2}$
D. $\sqrt{2}+\sqrt{8}=3\sqrt{2}$

答案： D

3. 计算$\sqrt{45}÷3\sqrt{2}×\sqrt{\frac{2}{5}}$的结果是 （ ）
A. 1
B. 2.5
C. 5
D. 6

答案： A

4. 已知$A(-1,y_1)$、$B(2,y_2)$两点在反比例函数$y=\frac{2m + 4}{x}$的图像上，且$y_1＞y_2$，则$m$的取值范围是 （ ）
A. $m＜-2$
B. $m＞-2$
C. $m＜0$
D. $m＞0$

答案： A

5. 如图，双曲线$y=\frac{k}{x}$经过点$A(2,4)$、$B(4,m)$，则$\triangle AOB$的面积为 （ ）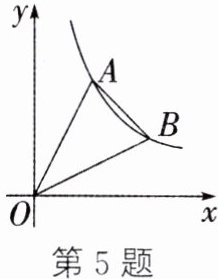
A. 3
B. 4
C. 5
D. 6

答案： D

6. 化简$\frac{\sqrt{12}}{\sqrt{2a}}(a＞0)$的结果是 ________.

答案： $\frac{\sqrt{6a}}{a}$

7. 计算：$\sqrt{80}-\sqrt{20}+\sqrt{5}=$________.

答案： $3\sqrt{5}$

8. 计算$\sqrt{\frac{y}{5}}÷\sqrt{\frac{y}{20x^3}}(x＞0,y＞0)$的结果是 ________.

答案： $2x\sqrt{x}$

9. 如图，设$P$是函数$y=\frac{4}{x}$在第一象限内的图像上的任意一点，点$P$关于原点的对称点为$P'$，过点$P$作$PA// y$轴，过点$P'$作$P'A// x$轴，$PA$与$P'A$相交于点$A$，则$\triangle PAP'$的面积是 ________.

答案： 8