《2025年全优课堂七年级数学上册人教版》

12. 下列单项式与$3x^{2}y$是同类项的是(C)
A.$-3xy$
B.$3x^{2}yz$
C.$2x^{2}y$
D.$3xy^{2}$

答案： C

13. 若$x\neq0$,$y\neq0$,且$\frac{1}{4}x^{2}y^{3}+ky^{3}x^{2}= 0$,则$k$的值是$-\frac {1}{4}$。

答案： $-\frac {1}{4}$

14. 若单项式$5x^{m + 1}y^{3}$与$-3x^{2}y^{n}$的和仍是单项式,则$m - n = $-2。

答案： -2

15. 若$-4x^{a}y + x^{2}y^{b}= -3x^{2}y$总成立,则$-a + b = $-1。

答案： -1

16. 应用意识水库中的水位第一天连续上升了$b$h,平均每小时上升$2$cm,第二天连续下降了$b$h,平均每小时下降$0.25$cm,第三天连续下降了$b$h,平均每小时下降$2.5$cm,这三天水位总的变化是下降(选填“上升”或“下降”)了0.75bcm。

答案： 下降 0.75b

17. 先化简,再求值。
$x^{3}-2x^{2}+x - 4 - 2x^{3}+5x + 4$,其中$x = -2$。

答案： 解:原式=$(1-2)x^{3}-2x^{2}+(1+5)x+(-4+4)=-x^{3}-2x^{2}+6x,$当$x=-2$时,$-x^{3}-2x^{2}+6x=-(-2)^{3}-2×(-2)^{2}+6×(-2)=8-8-12=-12.$

18. 如果代数式$x^{4}+ax^{3}+3x^{2}+5x^{3}-7x^{2}+6x - 2 - bx^{2}合并同类项后不含x^{3}$,$x^{2}$项,求$3a - 2b$的值。

答案： 解:$x^{4}+ax^{3}+3x^{2}+5x^{3}-7x^{2}+6x-2-bx^{2}=x^{4}+(a+5)x^{3}+(3-7-b)x^{2}+6x-2,$由$x^{4}+ax^{3}+3x^{2}+5x^{3}-7x^{2}+6x-2-bx^{2}$合并同类项后不含$x^{3}$和$x^{2}$项,得$a+5=0,3-7-b=0$,所以$a=-5,b=-4$,所以$3a-2b=3×(-5)-2×(-4)=-7.$

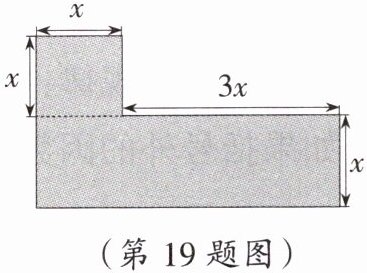
19. 数形结合思想如图,用含$x$的式子表示下面图形的面积,当$x = 12$cm 时,图形的面积是多少？

答案： 解:图形的面积可以分割成两块来计算,上面一块正方形,下面一块长方形,正方形的面积为$x^{2}$,长方形的长为$3x+x=4x$,宽为x,则面积为$4x\cdot x=4x^{2}$,则整个图形的面积为$x^{2}+4x^{2}=5x^{2}$.当$x=12cm$时,$5x^{2}=5×12^{2}=720$,因此当$x=12cm$时,图形面积为$720cm^{2}.$

20. 阅读理解新定义问题定义：若$A - B = m$,则称$A与B是关于m$的关联数。例如,若$A - B = 2$,则称$A与B是关于2$的关联数。
(1)若$4与a是关于7$的关联数,求$a$的值；
(2)若$M与N是关于m$的关联数,$M = 3mn + n + 3$,$N的值与m$无关,求$N$的值。

答案： 解:
(1)因为4与a是关于7的关联数,所以$4-a=7$,所以$a=-3;$
(2)因为M与N是关于m的关联数,所以$M-N=m$,所以$N=M-m,$因为$M=3mn+n+3$,所以$N=3mn+n+3-m=(3n-1)m+3+n$,因为N的值与m无关,所以$3n-1=0$,所以$n=\frac {1}{3}$,所以$N=(3n-1)m+3+n=3+\frac {1}{3}=3\frac {1}{3}.$

21. 讨论探究推理能力数学课上,张老师出示了这样一道题：“求多项式$7a^{3}+3a^{2}b + 3a^{3}+6a^{3}b - 3a^{2}b - 10a^{3}-6a^{3}b - 1$的值,其中$a = 2024$,$b = -2$。”小雅同学思索片刻后指出：“$a = 2024$,$b = -2$是多余的条件。”师生讨论后,一致认为小雅的说法是正确的,请你说明正确的理由。
解:$7a^{3}+3a^{2}b+3a^{3}+6a^{3}b-3a^{2}b-10a^{3}-6a^{3}b-1=7a^{3}+3a^{3}-10a^{3}+3a^{2}b-3a^{2}b+6a^{3}b-6a^{3}b-1=-1$,因为多项式$7a^{3}+3a^{2}b+3a^{3}+6a^{3}b-3a^{2}b-10a^{3}-6a^{3}b-1$化简后不含有a和b,所以多项式的值与a,b无关,所以小雅的说法是正确的.

答案： 解:$7a^{3}+3a^{2}b+3a^{3}+6a^{3}b-3a^{2}b-10a^{3}-6a^{3}b-1=7a^{3}+3a^{3}-10a^{3}+3a^{2}b-3a^{2}b+6a^{3}b-6a^{3}b-1=-1$,因为多项式$7a^{3}+3a^{2}b+3a^{3}+6a^{3}b-3a^{2}b-10a^{3}-6a^{3}b-1$化简后不含有a和b,所以多项式的值与a,b无关,所以小雅的说法是正确的.