第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
10. 若$a$,$b$互为相反数,且$c是绝对值为1$的数,则$a + b - c$的值是(
A.$1$
B.$-1$
C.$\pm1$
D.$0$
C
)A.$1$
B.$-1$
C.$\pm1$
D.$0$
答案:
C
11. 缺项型问题王博在做课外习题时遇到如图所示的一道题,其中 是被污损而看不清的一个数,它翻看答案后得知该题的计算结果为$15$,则
是被污损而看不清的一个数,它翻看答案后得知该题的计算结果为$15$,则 表示的数是(
表示的数是(
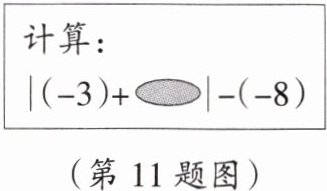
A.$10$
B.$-4$
C.$-10$
D.$10或-4$
 是被污损而看不清的一个数,它翻看答案后得知该题的计算结果为$15$,则
是被污损而看不清的一个数,它翻看答案后得知该题的计算结果为$15$,则 表示的数是(
表示的数是(D
)
A.$10$
B.$-4$
C.$-10$
D.$10或-4$
答案:
D
12. 定义新运算问题小明在电脑中设置了一个有理数的运算程序:$a*b = a - b + 5$,例如$(-3)*2 = (-3) - 2 + 5 = 0$,则$3*[4*(-5)]$的值为
-6
。
答案:
-6
13. 阅读下面的解题过程并解决问题:
计算:$53.27 - (-18) + (-21) + 46.73 - (+15) + 21$
解:原式$= 53.27 + 18 - 21 + 46.73 - 15 + 21$(第一步)
$= (53.27 + 46.73) + (21 - 21) + (18 - 15)$(第二步)
$= 100 + 0 + 3$(第三步)
$= 103$
(1)计算过程中,第一步把原式化成
(2)根据以上解题技巧计算下列式子:
$-21\frac{2}{3} + 3\frac{1}{4} - (-\frac{2}{3}) - (+ \frac{1}{4})$。
计算:$53.27 - (-18) + (-21) + 46.73 - (+15) + 21$
解:原式$= 53.27 + 18 - 21 + 46.73 - 15 + 21$(第一步)
$= (53.27 + 46.73) + (21 - 21) + (18 - 15)$(第二步)
$= 100 + 0 + 3$(第三步)
$= 103$
(1)计算过程中,第一步把原式化成
省略加号和括号
的形式,体现了数学中的转化
思想,为了计算简便,第二步应用了加法的交换律和结合律
;(2)根据以上解题技巧计算下列式子:
$-21\frac{2}{3} + 3\frac{1}{4} - (-\frac{2}{3}) - (+ \frac{1}{4})$。
解:$-21\frac{2}{3}+3\frac{1}{4}-(-\frac{2}{3})-(+\frac{1}{4})=-21\frac{2}{3}+3\frac{1}{4}+\frac{2}{3}-\frac{1}{4}=(-21\frac{2}{3}+\frac{2}{3})+(+3\frac{1}{4}-\frac{1}{4})=-21+3=-18$
答案:
解:
(1)省略加号和括号 转化 加法的交换律和结合律
(2)$-21\frac{2}{3}+3\frac{1}{4}-(-\frac{2}{3})-(+\frac{1}{4})=-21\frac{2}{3}+3\frac{1}{4}+\frac{2}{3}-\frac{1}{4}=(-21\frac{2}{3}+\frac{2}{3})+(+3\frac{1}{4}-\frac{1}{4})=-21+3=-18$.
(1)省略加号和括号 转化 加法的交换律和结合律
(2)$-21\frac{2}{3}+3\frac{1}{4}-(-\frac{2}{3})-(+\frac{1}{4})=-21\frac{2}{3}+3\frac{1}{4}+\frac{2}{3}-\frac{1}{4}=(-21\frac{2}{3}+\frac{2}{3})+(+3\frac{1}{4}-\frac{1}{4})=-21+3=-18$.
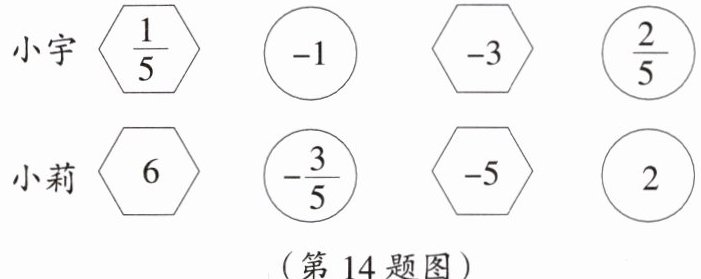
14. 中考新考法游戏问题在一次班会上,主持人小宇和小莉进行小游戏,游戏规则如下:每人每次抽$4$张卡片,如果抽到的形状为“”,那么加上卡片上的数字;如果抽到的形状为“”,那么减去卡片上的数字。最终计算结果小的为大家表演节目。小宇和小莉抽取的卡片如图所示,本次游戏结束后由谁给大家表演节目呢?
]
]

答案:
解:小宇:$\frac{1}{5}-(-1)+(-3)-\frac{2}{5}=\frac{1}{5}+1-3-\frac{2}{5}=-\frac{11}{5}$;小莉:$6-(-\frac{3}{5})+(-5)-2=6+\frac{3}{5}-5-2=-\frac{2}{5}$;因为$-\frac{11}{5}<-\frac{2}{5}$,所以本次游戏结束后由小宇给大家表演节目.
15. 中考新趋势联系生活实际足球比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:$m$):$+10$,$-2$,$+5$,$-6$,$+12$,$-9$,$+4$,$-14$。(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过$10m$(不包括$10m$),则对方球员挑射极可能造成破门。请问在这一时间段内,对方球员有几次挑射破门的机会?
解:
(1)+10-2+5-6+12-9+4-14=0,答:守门员最后正好回到球门线上;
(2)第一次10 m,第二次10-2=8(m),第三次8+5=13(m),第四次13-6=7(m),第五次7+12=19(m),第六次19-9=10(m),第七次10+4=14(m),第八次14-14=0(m),19>14>13>10>8>7.答:守门员离开球门线的最远距离达19 m;
(3)第一次10=10,第二次10-2=8<10,第三次8+5=13>10,第四次13-6=7<10,第五次7+12=19>10,第六次19-9=10,第七次10+4=14>10,第八次14-14=0,答:对方球员有三次挑射破门的机会.
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过$10m$(不包括$10m$),则对方球员挑射极可能造成破门。请问在这一时间段内,对方球员有几次挑射破门的机会?
解:
(1)+10-2+5-6+12-9+4-14=0,答:守门员最后正好回到球门线上;
(2)第一次10 m,第二次10-2=8(m),第三次8+5=13(m),第四次13-6=7(m),第五次7+12=19(m),第六次19-9=10(m),第七次10+4=14(m),第八次14-14=0(m),19>14>13>10>8>7.答:守门员离开球门线的最远距离达19 m;
(3)第一次10=10,第二次10-2=8<10,第三次8+5=13>10,第四次13-6=7<10,第五次7+12=19>10,第六次19-9=10,第七次10+4=14>10,第八次14-14=0,答:对方球员有三次挑射破门的机会.
答案:
解:
(1)+10-2+5-6+12-9+4-14=0,答:守门员最后正好回到球门线上;
(2)第一次10 m,第二次10-2=8(m),第三次8+5=13(m),第四次13-6=7(m),第五次7+12=19(m),第六次19-9=10(m),第七次10+4=14(m),第八次14-14=0(m),19>14>13>10>8>7.答:守门员离开球门线的最远距离达19 m;
(3)第一次10=10,第二次10-2=8<10,第三次8+5=13>10,第四次13-6=7<10,第五次7+12=19>10,第六次19-9=10,第七次10+4=14>10,第八次14-14=0,答:对方球员有三次挑射破门的机会.
(1)+10-2+5-6+12-9+4-14=0,答:守门员最后正好回到球门线上;
(2)第一次10 m,第二次10-2=8(m),第三次8+5=13(m),第四次13-6=7(m),第五次7+12=19(m),第六次19-9=10(m),第七次10+4=14(m),第八次14-14=0(m),19>14>13>10>8>7.答:守门员离开球门线的最远距离达19 m;
(3)第一次10=10,第二次10-2=8<10,第三次8+5=13>10,第四次13-6=7<10,第五次7+12=19>10,第六次19-9=10,第七次10+4=14>10,第八次14-14=0,答:对方球员有三次挑射破门的机会.
查看更多完整答案,请扫码查看


