《2025年全优课堂七年级数学上册人教版》

6. 应用意识某校组织七、八年级全体同学参观某爱国主义教育基地。七年级租用$45座大巴车x$辆,$55座大巴车y$辆；八年级租用$30座中巴车y$辆,$55座大巴车x$辆。当每辆车恰好坐满学生时,七年级有学生45x+55y名,八年级有学生55x+30y名。(用含$x$,$y$的代数式表示)

答案： (45x+55y)(55x+30y)

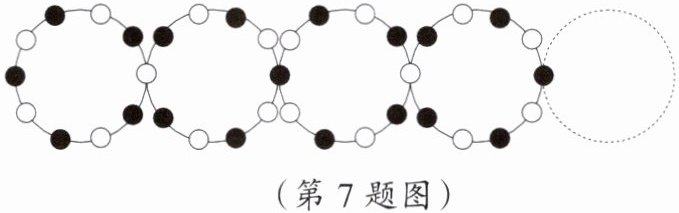
7. 如图,用$5$个实心圆圈、$5$个空心圆圈相间组成一个圆环,然后把这样的圆环从左到右按下列规律组成圆环串：相邻两圆环有一公共圆圈,公共圆圈从左到右以实心圆圈和空心圆圈相间排列。
(1)把表格补充完整：

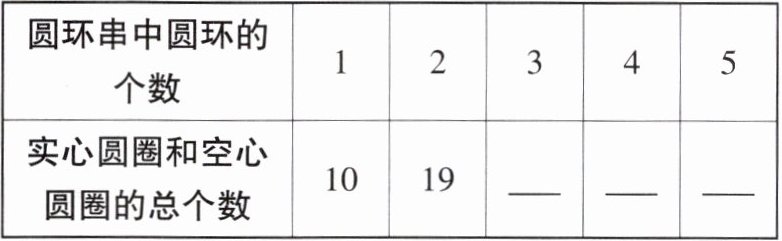
(2)设圆环串由$x$个圆环组成,请你直接写出组成这个圆环串所需实心圆圈和空心圆圈的总个数：9x+1(用含$x$的代数式表示)；
(3)如果圆环串由这样的$18$个圆环组成,那么实心圆圈和空心圆圈的总数有多少个？有多少个空心圆圈？

答案： 解:
(1)表格补充完整如下：
圆环串中圆环的个数 1 2 3 4 5
实心圆圈和空心圆圈的总个数 10 19 28 37 46
(2)9x+1 提示:因为每增加一个圆环,实心圆圈和空心圆圈的总个数就多9,所以当圆环串由x个圆环组成,组成圆环所需实心圆圈和空心圆圈的总个数为9x+1；
(3)当x=18时,实心圆圈和空心圆圈的总数有9×18+1=163(个),因为由偶数个圆环组成圆环串时需要的实心圆圈比空心圆圈多1个,所以空心圆圈有$\frac{163-1}{2}$=81(个).

8. 某校餐厅计划购买一批餐桌和餐椅。现从甲、乙两个商场了解到：同一型号的餐桌报价每张均为$200$元,餐椅报价每把均为$50$元。某商店开展促销活动,可以向顾客提供两种优惠方案：
方案一：每购买一张餐桌赠送一把餐椅。
方案二：所有餐桌、餐椅均按报价的$90\%$付款。
现某班要购买餐桌$20$张,餐椅$x$把($x超过20$)。
(1)若按方案一购买,需付款50x+3000元；若该班按方案二购买,需付款____45x+3600元(用含有$x$的式子表示)；
(2)当$x = 30$时,哪种方案更划算？请通过计算说明理由；
(3)若两种方案可以同时使用,当$x = 40$时,你能给出一种最省钱的购买方案吗？试写出你的购买方案,并计算该方案所需要的付款金额。

答案： 解:
(1)(50x+3000)(45x+3600) 提示:由题意得方案一:200×20+50(x-20)=(50x+3000)元；方案二:0.9(200×20+50x)=(45x+3600)元；
(2)方案一更划算,理由如下:当x=30时,方案一的费用为50x+3000=50×30+3000=4500(元),方案二的费用为45x+3600=45×30+3600=4950(元),因为4500＜4950,所以方案一更划算；
(3)方案:用方案一购买20张餐桌(赠送20把餐椅),再用方案二购买20把餐椅,则20×200+20×50×0.9=4000+900=4900(元),即用方案一购买20张餐桌(赠送20把餐椅),再用方案二购买20把餐椅,付款金额为4900元.