第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
9. 定义新运算 定义新运算“$\otimes$”,规定:$a\otimes b = a^{2}-|b|$,则$(-2)\otimes(-1)$的运算结果为 (
A.$-5$
B.$-3$
C.$5$
D.$3$
D
)A.$-5$
B.$-3$
C.$5$
D.$3$
答案:
D
10. 程序计算 如图是一个计算程序,若输入$a的值为-1$,则输出的结果$b$为 (

A.$-5$
B.$-6$
C.$5$
D.$6$
A
)
A.$-5$
B.$-6$
C.$5$
D.$6$
答案:
A
11. 利用规律求末尾数字 观察下列等式:$3^{1}= 3,3^{2}= 9,3^{3}= 27,3^{4}= 81,3^{5}= 243,…$,根据这个规律,则$3^{1}+3^{2}+3^{3}+…+3^{2014}$的结果的末位数字是 (
A.$0$
B.$2$
C.$9$
D.$8$
B
)A.$0$
B.$2$
C.$9$
D.$8$
答案:
B
12. 仔细观察下列等式:$2^{2}-1 = 1×3;3^{2}-1 = 2×4;4^{2}-1 = 3×5;5^{2}-1 = 4×6;6^{2}-1 = 5×7;…$,这些等式反映出自然数间的某种运算规律。则第$99$个等式可表示为
100²-1=99×101
。
答案:
100²-1=99×101
13. 有理数的游戏应用 魔术表演风靡全国,小明同学也发明了一个魔术盒,当任意有理数对$(a,b)$进入其中时,会得到一个新的有理数:$a^{2}+b - 1$。例如把$(3,-2)$放入其中,就会得到$3^{2}+(-2)-1 = 6$。
(1)若将有理数对$(1,2)$放入其中,求得到的值;
(2)已知有理数对$(m,n)$,满足$|m + 3|+(n - 2)^{2}= 0$,若将有理数对$(m,n)$放入其中,求得到的值。
(1)若将有理数对$(1,2)$放入其中,求得到的值;
(2)已知有理数对$(m,n)$,满足$|m + 3|+(n - 2)^{2}= 0$,若将有理数对$(m,n)$放入其中,求得到的值。
答案:
解:
(1)把有理数对(1,2)代入$a^{2}+b-1$得,$1^{2}+2-1=2$;
(2)因为$|m+3|+(n-2)^{2}=0$,$|m+3|≥0$,$(n-2)^{2}≥0$,所以$m+3=0$,$n-2=0$,所以$m=-3$,$n=2$,将(-3,2)代入$a^{2}+b-1$,得$(-3)^{2}+2-1=10$.
(1)把有理数对(1,2)代入$a^{2}+b-1$得,$1^{2}+2-1=2$;
(2)因为$|m+3|+(n-2)^{2}=0$,$|m+3|≥0$,$(n-2)^{2}≥0$,所以$m+3=0$,$n-2=0$,所以$m=-3$,$n=2$,将(-3,2)代入$a^{2}+b-1$,得$(-3)^{2}+2-1=10$.
14. 有理数的数字规律 探索:
(x - 1)(x + 1)= x^{2}-1,
(x - 1)(x^{2}+x + 1)= x^{3}-1,
(x - 1)(x^{3}+x^{2}+x + 1)= x^{4}-1,
(x - 1)(x^{4}+x^{3}+x^{2}+x + 1)= x^{5}-1,
…(1)试求2^{6}+2^{5}+2^{4}+2^{3}+2^{2}+2 + 1的值;(2)观察(1)的结论,判断2^{2008}+2^{2007}+2^{2006}+…+2^{2}+2 + 1的值的个位数是几?
(x - 1)(x + 1)= x^{2}-1,
(x - 1)(x^{2}+x + 1)= x^{3}-1,
(x - 1)(x^{3}+x^{2}+x + 1)= x^{4}-1,
(x - 1)(x^{4}+x^{3}+x^{2}+x + 1)= x^{5}-1,
…(1)试求2^{6}+2^{5}+2^{4}+2^{3}+2^{2}+2 + 1的值;(2)观察(1)的结论,判断2^{2008}+2^{2007}+2^{2006}+…+2^{2}+2 + 1的值的个位数是几?
答案:
解:
(1)$2^{6}+2^{5}+2^{4}+2^{3}+2^{2}+2 + 1=1×(2^{6}+2^{5}+2^{4}+2^{3}+2^{2}+2 + 1)=(2-1)(2^{6}+2^{5}+2^{4}+2^{3}+2^{2}+2 + 1)=2^{7}-1$;
(2)由
(1)可得,$2^{2008}+2^{2007}+2^{2006}+…+2^{2}+2 + 1=2^{2009}-1$,分析可得:2的1次方个位是2,2的2次方个位是4,2的3次方个位是8,2的4次方个位是6,2的5次方个位是2,2的6次方个位是4,2的7次方个位是8,2的8次方个位是6,……,四个一组,依次循环,故可得$2^{2009}$的个位数字是2,则$2^{2008}+2^{2007}+2^{2006}+…+2^{2}+2 + 1$即$2^{2009}-1$的值的个位数是1.
(1)$2^{6}+2^{5}+2^{4}+2^{3}+2^{2}+2 + 1=1×(2^{6}+2^{5}+2^{4}+2^{3}+2^{2}+2 + 1)=(2-1)(2^{6}+2^{5}+2^{4}+2^{3}+2^{2}+2 + 1)=2^{7}-1$;
(2)由
(1)可得,$2^{2008}+2^{2007}+2^{2006}+…+2^{2}+2 + 1=2^{2009}-1$,分析可得:2的1次方个位是2,2的2次方个位是4,2的3次方个位是8,2的4次方个位是6,2的5次方个位是2,2的6次方个位是4,2的7次方个位是8,2的8次方个位是6,……,四个一组,依次循环,故可得$2^{2009}$的个位数字是2,则$2^{2008}+2^{2007}+2^{2006}+…+2^{2}+2 + 1$即$2^{2009}-1$的值的个位数是1.
15. 数字规律推理能力 十进制是用$0\sim9$这十个数字来表示数,满十进一,例:$212 = 2×10^{2}+1×10 + 2$;计算机常用二进制来表示字符代码,它是用$0和1$两个数来表示数,满二进一。例如,二进制数$10000$转化为十进制数:$1×2^{4}+0×2^{3}+0×2^{2}+0×2^{1}+0 = 16$。其他进制也有类似的算法。
(1)根据以上信息,将二进制数“$101110$”转化为十进制数;
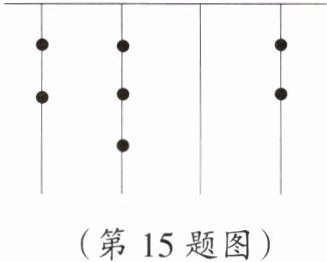
(2)中国古代《易经》一书中记载,人们通过在绳子上打结来记录数量,即“结绳记数”。如图,一位妇女在从右到左依次排列的绳子上打结,满六进一,用来记录采集到的野果数量。根据下图,计算采集到的野果数量。
(1)根据以上信息,将二进制数“$101110$”转化为十进制数;
(2)中国古代《易经》一书中记载,人们通过在绳子上打结来记录数量,即“结绳记数”。如图,一位妇女在从右到左依次排列的绳子上打结,满六进一,用来记录采集到的野果数量。根据下图,计算采集到的野果数量。

答案:
解:
(1)101110转化为十进制数是$1×2^{5}+0×2^{4}+1×2^{3}+1×2^{2}+1×2^{1}+0=32+0+8+4+2+0=46$;
(2)由于满六进一,类似于六进制数,转化为十进制数为$2×6^{3}+3×6^{2}+0×6^{1}+2=432+108+0+2=542$.
答:采集到的野果数量为542个.
(1)101110转化为十进制数是$1×2^{5}+0×2^{4}+1×2^{3}+1×2^{2}+1×2^{1}+0=32+0+8+4+2+0=46$;
(2)由于满六进一,类似于六进制数,转化为十进制数为$2×6^{3}+3×6^{2}+0×6^{1}+2=432+108+0+2=542$.
答:采集到的野果数量为542个.
查看更多完整答案,请扫码查看


