《2025年全优课堂七年级数学上册人教版》

23. (10 分)推理能力 观察下面三行数：
$ - 3 $,$ 9 $,$ - 27 $,$ 81 … … $ ①
$ 1 $,$ - 3 $,$ 9 $,$ - 27 … … $ ②
$ - 2 $,$ 10 $,$ - 26 $,$ 82 … … $ ③
(1)第①行数按什么规律排列？
(2)第②③行数与第①行数分别有什么关系？
(3)设 $ x $,$ y $,$ z $ 分别为①②③行的第 2 017 个数,求 $ x + 6 y + z $ 的值.

答案： 解:
(1)由-3,9,-27,81……可知第①行数是:(-3)¹,(-3)²,(-3)³,(-3)⁴,…,(-3)ⁿ;
(2)第②行数是第①行数相应的数乘$-\frac{1}{3},$即$-\frac{1}{3}×(-3)ⁿ,$第③行数比第①行相应的数大1,即(-3)ⁿ+1;
(3)因为$x=(-3)²⁰¹⁷,y=-\frac{1}{3}×(-3)²⁰¹⁷=(-3)²⁰¹⁶,z=(-3)²⁰¹⁷+1,$所以x+6y+z=(-3)²⁰¹⁷+6×(-3)²⁰¹⁶+(-3)²⁰¹⁷+1=1.

24. (11 分)抽象能力 小明同学积极参加体育锻炼,天天坚持跑步.他每天以 1 000 m 为标准,超过的记作正数,不足的记作负数.下表是一周内小明跑步情况的记录(单位：m)：

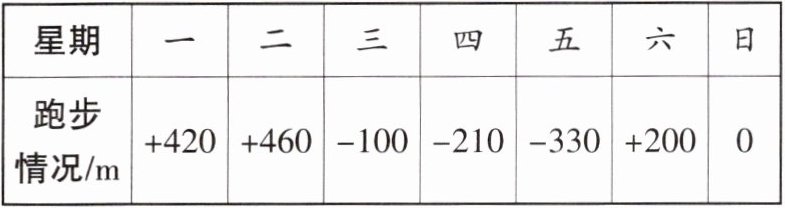
(1)星期三小明跑了多少米？
(2)小明跑得最少的一天跑了多少米？跑得最多的一天比最少的一天多跑了多少米？
(3)若小明跑步的平均速度为 $ 100 \mathrm { m } / \mathrm { min } $,求本周内小明用于跑步的时间.

答案： 解:
(1)星期三小明跑了1000-100=900(m);
(2)最少的一天跑了1000-330=670(m),跑得最多的一天比最少的一天多跑了460-(-330)=790(m);
(3)[(420+460-100-210-330+200)+1000×7]÷100=74.4(min).答:本周内小明用于跑步的时间为74.4 min.