第117页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
6. 习题变式 教材P148,T12改编 小亮和爸爸今年的年龄之和为36岁,再过5年,爸爸的年龄比小亮年龄的3倍大2岁,则小亮今年的年龄为 (
A.4岁
B.6岁
C.8岁
D.10岁
B
)A.4岁
B.6岁
C.8岁
D.10岁
答案:
B
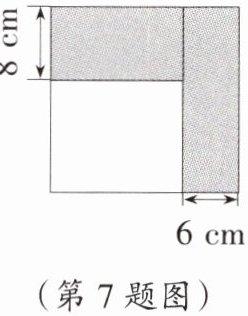
7. 习题变式 教材147,T5改编 如图,将一个正方形纸片剪去一个宽为6cm的长条后,再从剩下的长方形纸片上剪去一个宽为8cm的长条,如果两次剪去的长条的面积正好相等,那么每一个长条的面积为 (
$A. 20cm^2 B. 24cm^2 C. 48cm^2 D. 144cm^2$
D
)$A. 20cm^2 B. 24cm^2 C. 48cm^2 D. 144cm^2$

答案:
D
8. 数学文化 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格,将9个数填入幻方的空格中,要求九宫格中每一横行、每一竖列以及两条对角线上的3个数之和相等,如图是一个未完成的幻方,则x的值为 (
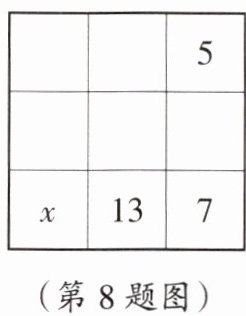
A.25
B.20
C.15
D.30
A
)
A.25
B.20
C.15
D.30
答案:
A
9. 为了加强公民的节水意识,合理利用水资源某市采用阶梯价格调控手段达到节水目的,价目表如下.

(1)某户居民1月用水$5.5m^3,$求1月的水费为多少元;
(2)若某户居民某月用水$x m^3,$则用含x的代数式表示该月所需交的水费;
(3)若某户居民5月共交水费22元,则该户居民5月实际用水多少立方米?

(1)某户居民1月用水$5.5m^3,$求1月的水费为多少元;
(2)若某户居民某月用水$x m^3,$则用含x的代数式表示该月所需交的水费;
(3)若某户居民5月共交水费22元,则该户居民5月实际用水多少立方米?
答案:
解:
(1)2×5.5=11(元).答:1月的水费为11元;
(2)当0<x≤6时,该月的水费为2x元;当6<x≤10时,该月的水费为2×6+4(x-6)=(4x-12)元;当x>10时,该月的水费为2×6+4×(10-6)+8(x-10)=(8x-52)元;
(3)因为2×6=12(元),2×6+4×(10-6)=28(元),12<22<28,所以该户居民5月实际用水量超过6 m³且不超过10 m³.根据题意得4x-12=22,解得x=8.5.答:该户居民5月实际用水8.5 m³.
(1)2×5.5=11(元).答:1月的水费为11元;
(2)当0<x≤6时,该月的水费为2x元;当6<x≤10时,该月的水费为2×6+4(x-6)=(4x-12)元;当x>10时,该月的水费为2×6+4×(10-6)+8(x-10)=(8x-52)元;
(3)因为2×6=12(元),2×6+4×(10-6)=28(元),12<22<28,所以该户居民5月实际用水量超过6 m³且不超过10 m³.根据题意得4x-12=22,解得x=8.5.答:该户居民5月实际用水8.5 m³.
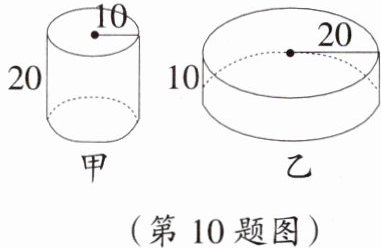
10. 数形结合思想 如图,有甲、乙两个容器,甲容器盛满水,乙容器里没有水,现将甲容器中的水全部倒入乙容器,问:水会不会溢出? 如果不会溢出,请你求出倒入水后乙容器中的水深;如果会溢出,请你说明理由.(容器壁厚度忽略不计,图中数据的单位:cm)

答案:
解:水不会溢出,设甲容器中的水全部倒入乙容器后,乙容器中的水深为x cm,由题意得π×10²×20=π×20²×x,解得x=5,所以甲容器中的水全部倒入乙容器后,乙容器中的水深为5 cm,因为5 cm<10 cm,所以水不会溢出.
11. 真实情境 应用意识 某中学需修理若干套库存桌椅,现让甲、乙两木工修理,甲每天修理桌椅16套,乙每天修理的桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲80元修理费,付乙120元修理费.
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a.由甲单独修理;b.由乙单独修理;c.甲、乙合作同时修理,你认为哪种方案省时又省钱? 为什么?
(1)设该中学库存x套桌椅,则$\frac{x}{16}-20=\frac{x}{16+8}$,解得x=960.答:该中学库存960套桌椅;
(2)方案c省时又省钱.理由:设a,b,c三种修理方案的费用分别为y₁,y₂,y₃元,则甲需修$\frac{960}{16}=60$(天),乙需修$\frac{960}{16+8}=40$(天),甲、乙合作需修$\frac{960}{16+16+8}=24$(天).则y₁=(80+10)×60=5400,y₂=(120+10)×40=5200,y₃=(80+120+10)×24=5040,因为5040<5200<5400,所以选择方案c更省时省钱.
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a.由甲单独修理;b.由乙单独修理;c.甲、乙合作同时修理,你认为哪种方案省时又省钱? 为什么?
(1)设该中学库存x套桌椅,则$\frac{x}{16}-20=\frac{x}{16+8}$,解得x=960.答:该中学库存960套桌椅;
(2)方案c省时又省钱.理由:设a,b,c三种修理方案的费用分别为y₁,y₂,y₃元,则甲需修$\frac{960}{16}=60$(天),乙需修$\frac{960}{16+8}=40$(天),甲、乙合作需修$\frac{960}{16+16+8}=24$(天).则y₁=(80+10)×60=5400,y₂=(120+10)×40=5200,y₃=(80+120+10)×24=5040,因为5040<5200<5400,所以选择方案c更省时省钱.
答案:
解:
(1)设该中学库存x套桌椅,则$\frac{x}{16}-20=\frac{x}{16+8}$,解得x=960.答:该中学库存960套桌椅;
(2)方案c省时又省钱.理由:设a,b,c三种修理方案的费用分别为y₁,y₂,y₃元,则甲需修$\frac{960}{16}=60$(天),乙需修$\frac{960}{16+8}=40$(天),甲、乙合作需修$\frac{960}{16+16+8}=24$(天).则y₁=(80+10)×60=5400,y₂=(120+10)×40=5200,y₃=(80+120+10)×24=5040,因为5040<5200<5400,所以选择方案c更省时省钱.
(1)设该中学库存x套桌椅,则$\frac{x}{16}-20=\frac{x}{16+8}$,解得x=960.答:该中学库存960套桌椅;
(2)方案c省时又省钱.理由:设a,b,c三种修理方案的费用分别为y₁,y₂,y₃元,则甲需修$\frac{960}{16}=60$(天),乙需修$\frac{960}{16+8}=40$(天),甲、乙合作需修$\frac{960}{16+16+8}=24$(天).则y₁=(80+10)×60=5400,y₂=(120+10)×40=5200,y₃=(80+120+10)×24=5040,因为5040<5200<5400,所以选择方案c更省时省钱.
查看更多完整答案,请扫码查看


