《2025年作业本江西教育出版社九年级数学全一册人教版》

1. 为了测得图①和图②中旗杆的高度,在太阳光下同一时刻,小明和小红分别测得竹竿$CD长0.9\ m$,其影长$CE为1\ m$。
(1)如图①所示,若小明测得旗杆影长$AE为3\ m$,求旗杆$AB$高为多少米($CD\perp AE$,$AB\perp AE$,$B,D,E$在同一条直线上)。
(2)如图②所示,若小红测得旗杆落在地面上的影长$FG为3\ m$,落在墙上的影子$GH的高为1.1\ m$,求旗杆$FP$高为多少米($PF\perp FG$,$HG\perp FG$)。

答案： 【解析】：本题主要考查相似三角形的性质，即同一时刻物高与影长成正比。
（1）对于图①，由于$CD\perp AE$，$AB\perp AE$，且太阳光线是平行的，所以$\triangle CDE$与$\triangle BAE$是相似三角形。
根据相似三角形的性质，我们有$\frac{CD}{AB}=\frac{CE}{AE}$。
代入已知条件$CD=0.9m$，$CE=1m$，$AE=3m$，我们可以求出$AB$。
（2）对于图②，我们可以先求出如果$GH$的影子完全落在地面上时的影长，然后再利用相似三角形的性质求出旗杆的高度。
设太阳光与地面的夹角为$\alpha$，则$\tan\alpha=\frac{CD}{CE}=\frac{0.9}{1}=0.9$。
当旗杆的影子完全落在地面上时，设影长为$x$，则$\frac{FP}{x}=\tan\alpha=0.9$。
但此时我们还需要考虑落在墙上的影子$GH$，所以实际的影长应该是$x+3$（其中3是$FG$的长度）。
而$FP$的高度应该是$0.9(x+3)$，同时$FP$还等于$1.1+0.9x$（其中1.1是$GH$的高度）。
【答案】：
(1)解：
∵同一时刻物高与影长成正比，
∴$\frac{AB}{AE}=\frac{CD}{CE}$
即$\frac{AB}{3}=\frac{0.9}{1}$
解得$AB=2.7m$。
(2)解：设从墙上的影子的顶端到旗杆的顶端的垂直高度为$x$米。
∵同一时刻物高与影长成正比，
∴$\frac{0.9}{1}=\frac{x}{3}$
解得$x=2.7$
∴旗杆的高度为$2.7+1.1=3.8$（米）。

2. 小颖想利用镜子与皮尺测量大树$AB$的高,因大树底部有障碍物,无法直接测量到大树底部的距离,于是她设计出下列测量方案：小颖站在点$F$处,将镜子放在点$M$处时,刚好看到大树的顶端,沿大树方向向前走$3\ m$,到达点$D$处,将镜子放在点$N$处时,刚好看到大树的顶端(点$F,M,D,N,B$在同一条直线上)。测得$FM= 1.5\ m$,$DN= 1\ m$,小颖眼睛到地面的距离为$1.6\ m$,如图所示。
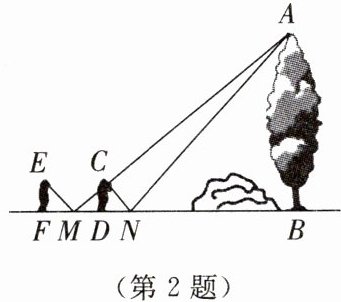
(1)求证：①$\triangle EFM\backsim\triangle ABM$；②$\triangle CDN\backsim\triangle ABN$。
(2)求大树的高$AB$。

答案：
(1)证明：①
∵EF⊥FB，AB⊥FB，
∴∠EFM=∠ABM=90°，
∵∠EMF=∠AMB（反射角等于入射角），
∴△EFM∽△ABM；
②
∵CD⊥FB，AB⊥FB，
∴∠CDN=∠ABN=90°，
∵∠CND=∠ANB（反射角等于入射角），
∴△CDN∽△ABN；
(2)解：设AB=x m，NB=y m，
由
(1)①得$\frac{EF}{AB}=\frac{FM}{BM}$，即$\frac{1.6}{x}=\frac{1.5}{1.5+1+y}$，
由
(1)②得$\frac{CD}{AB}=\frac{DN}{BN}$，即$\frac{1.6}{x}=\frac{1}{y}$，
联立得$\frac{1.5}{2.5+y}=\frac{1}{y}$，解得$y=5$，
代入$\frac{1.6}{x}=\frac{1}{5}$，得$x=8$，
答：大树的高AB为8 m。