第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
1. 神舟二十号出征仪式上,三名航天员进行合影,若随机站成一排,则航天员陈冬站在中间的概率为
$\frac{1}{3}$
.
答案:
解:三名航天员随机站成一排,所有可能的排列情况为:(陈冬,航天员A,航天员B)、(陈冬,航天员B,航天员A)、(航天员A,陈冬,航天员B)、(航天员A,航天员B,陈冬)、(航天员B,陈冬,航天员A)、(航天员B,航天员A,陈冬),共6种等可能的结果。
其中陈冬站在中间的情况有2种:(航天员A,陈冬,航天员B)、(航天员B,陈冬,航天员A)。
所以陈冬站在中间的概率为$P=\frac{2}{6}=\frac{1}{3}$。
$\frac{1}{3}$
其中陈冬站在中间的情况有2种:(航天员A,陈冬,航天员B)、(航天员B,陈冬,航天员A)。
所以陈冬站在中间的概率为$P=\frac{2}{6}=\frac{1}{3}$。
$\frac{1}{3}$
2. 若a,b可以分别取-1,1,2中任意一个值(a≠b),则直线y= ax+b的图象不经过第四象限的概率是
$\frac{1}{3}$
.
答案:
【解析】:
本题主要考察概率的计算以及一次函数图像的性质。
首先,我们需要确定$a, b$的所有可能取值组合,由于$a, b$可以分别取$-1, 1, 2$中的任意一个值,且$a \neq b$,
因此,总共有$3 × 2 = 6$种组合方式。
然后,我们需要分析一次函数$y = ax + b$的图像性质,要使图像不经过第四象限,
需要满足两个条件:斜率$a > 0$,截距$b \geq 0$。
接下来,我们列举出所有满足条件的$a, b$组合:
当$a = 1, b = 2$时,满足条件;
当$a = 2, b = 1$时,满足条件;
其他组合均不满足条件。
因此,满足条件的组合有2种,总共有6种组合方式,
所以直线$y = ax + b$的图象不经过第四象限的概率为$\frac{2}{6} = \frac{1}{3}$。
【答案】:
$\frac{1}{3}$。
本题主要考察概率的计算以及一次函数图像的性质。
首先,我们需要确定$a, b$的所有可能取值组合,由于$a, b$可以分别取$-1, 1, 2$中的任意一个值,且$a \neq b$,
因此,总共有$3 × 2 = 6$种组合方式。
然后,我们需要分析一次函数$y = ax + b$的图像性质,要使图像不经过第四象限,
需要满足两个条件:斜率$a > 0$,截距$b \geq 0$。
接下来,我们列举出所有满足条件的$a, b$组合:
当$a = 1, b = 2$时,满足条件;
当$a = 2, b = 1$时,满足条件;
其他组合均不满足条件。
因此,满足条件的组合有2种,总共有6种组合方式,
所以直线$y = ax + b$的图象不经过第四象限的概率为$\frac{2}{6} = \frac{1}{3}$。
【答案】:
$\frac{1}{3}$。
3. 现有四张分别标有数字1,2,2,3的卡片,它们除数字外无其他差别.若把卡片背面朝上洗匀,从中随机抽出一张后放回,再背面朝上洗匀,从中随机抽出一张,则两次抽出的卡片所标数字不同的概率是
$\frac{5}{8}$
.
答案:
解:列表如下:
| 第一次 | 1 | 2 | 2 | 3 |
| ---- | ---- | ---- | ---- | ---- |
| 1 | (1,1) | (1,2) | (1,2) | (1,3) |
| 2 | (2,1) | (2,2) | (2,2) | (2,3) |
| 2 | (2,1) | (2,2) | (2,2) | (2,3) |
| 3 | (3,1) | (3,2) | (3,2) | (3,3) |
共有16种等可能的结果,其中两次抽出的卡片所标数字不同的结果有10种,
所以两次抽出的卡片所标数字不同的概率是$\frac{10}{16}=\frac{5}{8}$。
答案:$\frac{5}{8}$
| 第一次 | 1 | 2 | 2 | 3 |
| ---- | ---- | ---- | ---- | ---- |
| 1 | (1,1) | (1,2) | (1,2) | (1,3) |
| 2 | (2,1) | (2,2) | (2,2) | (2,3) |
| 2 | (2,1) | (2,2) | (2,2) | (2,3) |
| 3 | (3,1) | (3,2) | (3,2) | (3,3) |
共有16种等可能的结果,其中两次抽出的卡片所标数字不同的结果有10种,
所以两次抽出的卡片所标数字不同的概率是$\frac{10}{16}=\frac{5}{8}$。
答案:$\frac{5}{8}$
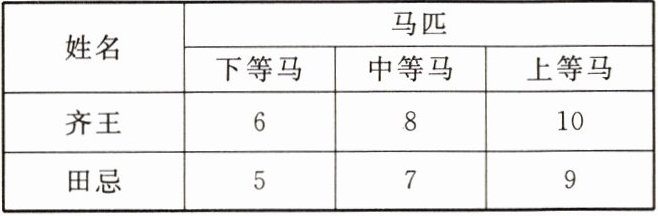
4. 看了《田忌赛马》的故事后,小杨用数学模型来分析:齐王与田忌的上、中、下三个等级的三匹马记分如下表所示,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为______
| 姓名 | 马匹 | 下等马 | 中等马 | 上等马 |
| 齐王 | | 6 | 8 | 10 |
| 田忌 | | 5 | 7 | 9 |
$\frac{1}{6}$
.| 姓名 | 马匹 | 下等马 | 中等马 | 上等马 |
| 齐王 | | 6 | 8 | 10 |
| 田忌 | | 5 | 7 | 9 |

答案:
解:齐王马匹出场顺序固定为10(上等)、8(中等)、6(下等)。
田忌三匹马(5,7,9)的所有出场顺序列举如下:
1. (5,7,9):对阵齐王(10,8,6),结果:5<10,7<8,9>6,胜1场,输。
2. (5,9,7):对阵齐王(10,8,6),结果:5<10,9>8,7>6,胜2场,赢。
3. (7,5,9):对阵齐王(10,8,6),结果:7<10,5<8,9>6,胜1场,输。
4. (7,9,5):对阵齐王(10,8,6),结果:7<10,9>8,5<6,胜1场,输。
5. (9,5,7):对阵齐王(10,8,6),结果:9<10,5<8,7>6,胜1场,输。
6. (9,7,5):对阵齐王(10,8,6),结果:9<10,7<8,5<6,胜0场,输。
共有6种等可能结果,其中田忌赢的结果有1种。
所以田忌能赢得比赛的概率为$\frac{1}{6}$。
答案:$\frac{1}{6}$
田忌三匹马(5,7,9)的所有出场顺序列举如下:
1. (5,7,9):对阵齐王(10,8,6),结果:5<10,7<8,9>6,胜1场,输。
2. (5,9,7):对阵齐王(10,8,6),结果:5<10,9>8,7>6,胜2场,赢。
3. (7,5,9):对阵齐王(10,8,6),结果:7<10,5<8,9>6,胜1场,输。
4. (7,9,5):对阵齐王(10,8,6),结果:7<10,9>8,5<6,胜1场,输。
5. (9,5,7):对阵齐王(10,8,6),结果:9<10,5<8,7>6,胜1场,输。
6. (9,7,5):对阵齐王(10,8,6),结果:9<10,7<8,5<6,胜0场,输。
共有6种等可能结果,其中田忌赢的结果有1种。
所以田忌能赢得比赛的概率为$\frac{1}{6}$。
答案:$\frac{1}{6}$
5. 小龙和小丽用“红桃3”“红桃4”和“黑桃5”这三张扑克牌玩游戏.将这三张扑克牌洗牌后反扣在桌面上,翻开一张记下花色,然后反扣洗牌,再翻开一张记下花色.若两次都是红桃,则小龙赢;若一次红桃一次黑桃,则小丽赢.小龙和小丽谁赢的可能性大?请说明理由.
答案:
解:
首先,计算所有可能的情况。
第一次翻牌有$3$种可能,第二次翻牌也有$3$种可能,根据排列组合的乘法原理,总共有$3×3 = 9$种可能的情况。
然后,计算小龙赢的情况(两次都是红桃)。
红桃有$2$张(红桃$3$、红桃$4$),第一次翻到红桃的概率是$\frac{2}{3}$,第二次翻到红桃的概率也是$\frac{2}{3}$,根据独立事件概率的乘法公式,小龙赢的概率$P_{龙}=\frac{2}{3}×\frac{2}{3}=\frac{4}{9}$。
接着,计算小丽赢的情况(一次红桃一次黑桃)。
分两种情况:
第一种情况:第一次红桃,第二次黑桃。概率$P_1=\frac{2}{3}×\frac{1}{3}=\frac{2}{9}$;
第二种情况:第一次黑桃,第二次红桃。概率$P_2=\frac{1}{3}×\frac{2}{3}=\frac{2}{9}$。
那么小丽赢的概率$P_{丽}=P_1 + P_2=\frac{2}{9}+\frac{2}{9}=\frac{4}{9}$。
所以小龙和小丽赢的可能性一样大。
首先,计算所有可能的情况。
第一次翻牌有$3$种可能,第二次翻牌也有$3$种可能,根据排列组合的乘法原理,总共有$3×3 = 9$种可能的情况。
然后,计算小龙赢的情况(两次都是红桃)。
红桃有$2$张(红桃$3$、红桃$4$),第一次翻到红桃的概率是$\frac{2}{3}$,第二次翻到红桃的概率也是$\frac{2}{3}$,根据独立事件概率的乘法公式,小龙赢的概率$P_{龙}=\frac{2}{3}×\frac{2}{3}=\frac{4}{9}$。
接着,计算小丽赢的情况(一次红桃一次黑桃)。
分两种情况:
第一种情况:第一次红桃,第二次黑桃。概率$P_1=\frac{2}{3}×\frac{1}{3}=\frac{2}{9}$;
第二种情况:第一次黑桃,第二次红桃。概率$P_2=\frac{1}{3}×\frac{2}{3}=\frac{2}{9}$。
那么小丽赢的概率$P_{丽}=P_1 + P_2=\frac{2}{9}+\frac{2}{9}=\frac{4}{9}$。
所以小龙和小丽赢的可能性一样大。
6. 某校准备从甲、乙2名女生和丙、丁2名男生中任选2人代表学校参加中学生“党史演讲”竞赛.
(1)若已经确定女生甲参加,再从其余的候选人中随机选取1人,则女生乙被选中的概率是
(2)用列表的方法,求出所选代表恰好为1名女生和1名男生的概率.
(1)若已经确定女生甲参加,再从其余的候选人中随机选取1人,则女生乙被选中的概率是
$\frac{1}{3}$
.(2)用列表的方法,求出所选代表恰好为1名女生和1名男生的概率.
解:列出所有可能的组合:甲、乙;甲、丙;甲、丁;乙、丙;乙、丁;丙、丁,共6种。满足1名女生和1名男生的组合有甲、丙;甲、丁;乙、丙;乙、丁,共4种。所以概率为$\frac{4}{6}=\frac{2}{3}$。
答案:
【解析】:
本题主要考察概率的计算,特别是使用列举法来求概率。
(1) 对于第一个问题,已经确定女生甲参加,那么只需要从乙、丙、丁中选一人。这里涉及到简单概率的计算,即事件发生的次数除以所有可能事件的次数。
(2) 对于第二个问题,需要列出所有可能的组合,并计算满足条件(即一男一女)的组合的概率。
【答案】:
(1) 解:
已经确定女生甲参加,那么从乙、丙、丁中随机选取一人的概率空间为 {乙, 丙, 丁}。因此,女生乙被选中的概率为 $\frac{1}{3}$。
(2) 解:
首先,我们列出所有可能的组合:
甲、乙
甲、丙
甲、丁
乙、丙
乙、丁
丙、丁
总共有6种组合。
接着,我们找出满足条件(一男一女)的组合:
甲、丙
甲、丁
乙、丙
乙、丁
共有4种组合。
所以,所选代表恰好为1名女生和1名男生的概率为 $\frac{4}{6} = \frac{2}{3}$。
本题主要考察概率的计算,特别是使用列举法来求概率。
(1) 对于第一个问题,已经确定女生甲参加,那么只需要从乙、丙、丁中选一人。这里涉及到简单概率的计算,即事件发生的次数除以所有可能事件的次数。
(2) 对于第二个问题,需要列出所有可能的组合,并计算满足条件(即一男一女)的组合的概率。
【答案】:
(1) 解:
已经确定女生甲参加,那么从乙、丙、丁中随机选取一人的概率空间为 {乙, 丙, 丁}。因此,女生乙被选中的概率为 $\frac{1}{3}$。
(2) 解:
首先,我们列出所有可能的组合:
甲、乙
甲、丙
甲、丁
乙、丙
乙、丁
丙、丁
总共有6种组合。
接着,我们找出满足条件(一男一女)的组合:
甲、丙
甲、丁
乙、丙
乙、丁
共有4种组合。
所以,所选代表恰好为1名女生和1名男生的概率为 $\frac{4}{6} = \frac{2}{3}$。
查看更多完整答案,请扫码查看


