《2025年作业本江西教育出版社九年级数学全一册人教版》

1. 如图所示,该图案可以看作由其中一个菱形至少经过5次旋转得到的,旋转角的大小是60°.

答案： 1. 首先分析旋转次数：
观察图形可知，该图案由$6$个菱形组成，所以可以看作由其中一个菱形至少经过$5$次旋转得到。
2. 然后求旋转角的大小：
因为整个圆周角是$360^{\circ}$，且$6$个菱形组成一个周角，所以旋转角$\theta=\frac{360^{\circ}}{6}=60^{\circ}$。
故答案依次为：$5$；$60^{\circ}$。

2. 如图所示,△ABC绕点C顺时针旋转37°后得到△A'B'C.若A'B'⊥AC于点D,则∠A= 53°.

答案： 【解析】：本题主要考查了图形旋转的性质。
根据旋转的性质可知，旋转前后对应角相等，旋转角也相等。
已知$\bigtriangleup ABC$绕点$C$顺时针旋转$37^{\circ}$后得到$\bigtriangleup A'B'C$，所以$\angle ACA' = 37^{\circ}$，且$\angle A=\angle A'$。
因为$A'B'\perp AC$于点$D$，所以在$Rt\bigtriangleup A'DC$中，$\angle A'DC = 90^{\circ}$。
根据三角形内角和为$180^{\circ}$，在$\bigtriangleup A'DC$中，$\angle A' = 180^{\circ}-\angle A'DC-\angle ACA'=180^{\circ}- 90^{\circ}-37^{\circ}=53^{\circ}$。
又因为$\angle A=\angle A'$，所以$\angle A = 53^{\circ}$。
【答案】：$53^{\circ}$

3. 如图所示,在平面直角坐标系中,边长为2个单位长度的正方形ABCO绕原点O逆时针旋转75°,再沿y轴方向向上平移1个单位长度,则点B''的坐标为______.

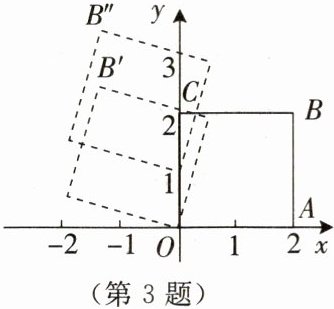
(-√2, √6+1)

答案： 解：
∵正方形ABCO边长为2，
∴点B坐标为(2,2)，OB=√(2²+2²)=2√2，OB与x轴夹角为45°。
绕原点O逆时针旋转75°后，OB'与x轴夹角为45°+75°=120°，OB'=2√2。
点B'坐标：
x=2√2·cos120°=2√2·(-1/2)=-√2，
y=2√2·sin120°=2√2·(√3/2)=√6。
沿y轴向上平移1个单位后，点B''坐标为(-√2, √6+1)。
(-√2, √6+1)

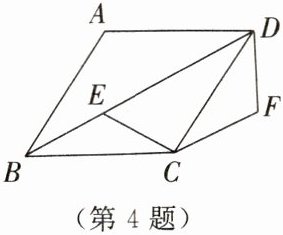
4. 如图所示,在菱形ABCD中,∠BCD= 120°,点E在对角线BD上,将线段CE绕点C顺时针旋转120°,得到CF,连接DF.
(1)求证：△BCE≌△DCF.
(2)若BC= 4,求四边形ECFD的面积.

答案： 【解析】：
(1)证明题，需要证明两个三角形全等。根据题目条件，我们知道菱形ABCD中，∠BCD=120°，点E在对角线BD上，线段CE绕点C顺时针旋转120°得到CF，连接DF。我们需要证明△BCE≌△DCF。
首先，由于ABCD是菱形，所以BC=CD，∠BCD=120°，因此∠BCE+∠ECD=120°。又因为线段CE绕点C顺时针旋转120°得到CF，所以∠ECF=120°，从而∠DCF+∠ECD=120°。由此可得∠BCE=∠DCF。另外，CE=CF（旋转得到）。所以，根据SAS（边角边）全等条件，△BCE≌△DCF。
(2)接下来求四边形ECFD的面积。由于△BCE≌△DCF，所以四边形ECFD的面积等于△BCD的面积（因为ECFD可以看作是由BCE和DCF两个全等的三角形组成，而这两个三角形的面积之和等于BCD的面积）。在菱形ABCD中，∠BCD=120°，所以∠B=60°（菱形对角线互相垂直且平分对角，所以∠B和∠D都是60°）。又因为BC=CD=4（菱形四边等长），所以△BCD是等边三角形（两边相等且夹角为60°的三角形是等边三角形）。等边三角形的面积公式为$\frac{\sqrt{3}}{4}a^2$，其中a为边长。代入a=4，得到$S_{△BCD}=\frac{\sqrt{3}}{4}×4^2=4\sqrt{3}$。所以，四边形ECFD的面积也为$4\sqrt{3}$。
【答案】：
(1)证明：
∵ABCD为菱形，
∴BC=CD，∠BCD=120°，
∴∠BCE+∠ECD=120°，
∵线段CE绕点C顺时针旋转120°得到CF，
∴∠ECF=120°，
∴∠DCF+∠ECD=120°，
∴∠BCE=∠DCF，
∵CE=CF，
∴△BCE≌△DCF（SAS）。
(2)解：
∵△BCE≌△DCF，
∴$S_{ECFD}=S_{△BCD}$，
∵BC=CD，∠BCD=120°，
∴∠B=60°，
∴△BCD为等边三角形，
∴$S_{△BCD}=\frac{\sqrt{3}}{4}×4^2=4\sqrt{3}$，
∴$S_{ECFD}=4\sqrt{3}$。

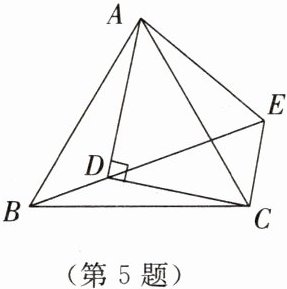
5. 如图所示,已知在等边三角形ABC中,D为△ABC内的一点,∠ADB= 120°,∠ADC= 90°.将△ABD绕点A逆时针旋转60°得到△ACE,连接DE.
(1)求证：AD= DE.
(2)求∠DCE的大小.
(3)若BD= 1,求CD的长.

答案：
(1)证明：
∵将△ABD绕点A逆时针旋转60°得到△ACE，
∴AD=AE，∠DAE=60°，
∴△ADE是等边三角形，
∴AD=DE；
(2)解：
∵△ABC是等边三角形，
∴∠BAC=60°，
∵将△ABD绕点A逆时针旋转60°得到△ACE，
∴∠BAD=∠CAE，∠AEC=∠ADB=120°，BD=CE=1，
∵∠BAC=∠BAD+∠DAC=60°，
∴∠DAE=∠CAE+∠DAC=60°，
∵∠ADC=90°，∠AEC=120°，
∴∠DCE=360°-∠ADC-∠AEC-∠DAE=360°-90°-120°-60°=90°；
(3)解：由
(1)知△ADE是等边三角形，
∴DE=AD，
由
(2)知∠DCE=90°，CE=BD=1，
设CD=x，AD=DE=y，
在Rt△CDE中，CD²+CE²=DE²，
∴x²+1²=y²，
在Rt△ADC中，AD²+CD²=AC²，
∵△ABC是等边三角形，
∴AC=AB，
由旋转知AE=AD=y，CE=BD=1，
在△ABD中，AB²=AD²+BD²-2·AD·BD·cos∠ADB，
∠ADB=120°，
∴AB²=y²+1²-2·y·1·cos120°=y²+1+ y，
∵AC=AB，
∴y²+ x²=y²+1+ y，
∴x²=1+ y，
∵x²+1=y²，
∴y²-1=1+ y，
∴y²-y-2=0，
解得y=2或y=-1(舍去)，
∴y=2，
∴x²=1+2=3，
∴x=√3，
即CD=√3.