第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
1. 如图所示,$AB为\odot O$的直径,弦$CD\perp AB于点E$. 若$CD= 8$,$OE= 3$,则$\odot O$的半径为
5
.
答案:
解:连接OC。
∵AB为⊙O的直径,CD⊥AB于点E,CD=8,
∴CE=CD/2=4,∠OEC=90°。
设⊙O的半径为r,则OC=r,OE=3。
在Rt△OEC中,由勾股定理得:OC²=OE²+CE²,
即r²=3²+4²,解得r=5。
故⊙O的半径为5。
∵AB为⊙O的直径,CD⊥AB于点E,CD=8,
∴CE=CD/2=4,∠OEC=90°。
设⊙O的半径为r,则OC=r,OE=3。
在Rt△OEC中,由勾股定理得:OC²=OE²+CE²,
即r²=3²+4²,解得r=5。
故⊙O的半径为5。
2. 如图所示,$\odot O的半径为13$,$AB= 24$. 若点$P在弦AB$上运动,则$OP$的取值范围是
5≤OP≤13
.
答案:
解:过点O作OC⊥AB于点C,连接OA。
∵OC⊥AB,AB=24,
∴AC=BC=12。
在Rt△OAC中,OA=13,AC=12,
由勾股定理得:OC=$\sqrt{OA^2 - AC^2}=\sqrt{13^2 - 12^2}=5$。
∵点P在弦AB上运动,
∴当P与C重合时,OP最短,OP=OC=5;
当P与A或B重合时,OP最长,OP=OA=13。
∴OP的取值范围是5≤OP≤13。
答案:5≤OP≤13
∵OC⊥AB,AB=24,
∴AC=BC=12。
在Rt△OAC中,OA=13,AC=12,
由勾股定理得:OC=$\sqrt{OA^2 - AC^2}=\sqrt{13^2 - 12^2}=5$。
∵点P在弦AB上运动,
∴当P与C重合时,OP最短,OP=OC=5;
当P与A或B重合时,OP最长,OP=OA=13。
∴OP的取值范围是5≤OP≤13。
答案:5≤OP≤13
3. 如图所示,这是一个隧道的横截面,它的形状是以点$O$为圆心的圆的一部分. 如果$C是\odot O中弦AB$的中点,$CD经过圆心O交\odot O于点D$,并且$AB= 4\ m$,$CD= 6\ m$,那么$\odot O$的半径长为
$\frac{10}{3}$
$m$.
答案:
【解析】:
本题主要考查了圆的性质以及勾股定理的应用。
连接$OA$。
设$\odot O$的半径为$r$,
$\because C$是$\overset{\frown}{AB}$的中点,且$CD$经过圆心$O$,
根据圆的垂径定理:垂直于弦的直径平分弦且平分这条弦所对的两条弧
$\therefore CD\perp AB$,$AC=\frac{1}{2}AB=2$(m),
$\therefore$在$Rt\triangle AOC$中,$OC=CD-OD=6-r$,
$\because OA^{2}=AC^{2}+OC^{2}$,即$r^{2}=2^{2}+(6-r)^{2}$,解得$r=\frac{10}{3}$。
【答案】:
$\frac{10}{3}$。
本题主要考查了圆的性质以及勾股定理的应用。
连接$OA$。
设$\odot O$的半径为$r$,
$\because C$是$\overset{\frown}{AB}$的中点,且$CD$经过圆心$O$,
根据圆的垂径定理:垂直于弦的直径平分弦且平分这条弦所对的两条弧
$\therefore CD\perp AB$,$AC=\frac{1}{2}AB=2$(m),
$\therefore$在$Rt\triangle AOC$中,$OC=CD-OD=6-r$,
$\because OA^{2}=AC^{2}+OC^{2}$,即$r^{2}=2^{2}+(6-r)^{2}$,解得$r=\frac{10}{3}$。
【答案】:
$\frac{10}{3}$。
4. 如图所示,方格纸上每个小正方形的边长均为$1$个单位长度,点$O,A,B,C$在格点上. 若以点$O$为原点建立平面直角坐标系,则过$A,B,C$三点的圆的圆心坐标为
$(-1,-2)$
.
答案:
$(-1,-2)$
5. 如图所示,$OA= OB$,$AB交\odot O于点C,D$,$AC与BD$是否相等?为什么?
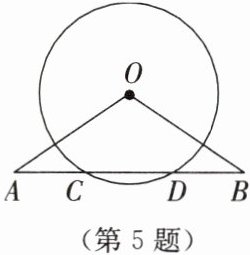

答案:
解:AC=BD。
过点O作OE⊥AB于点E。
∵OE⊥AB,
∴CE=DE(垂径定理)。
∵OA=OB,OE⊥AB,
∴AE=BE(等腰三角形三线合一)。
∵AE-CE=BE-DE,
∴AC=BD。
过点O作OE⊥AB于点E。
∵OE⊥AB,
∴CE=DE(垂径定理)。
∵OA=OB,OE⊥AB,
∴AE=BE(等腰三角形三线合一)。
∵AE-CE=BE-DE,
∴AC=BD。
6. 一根横截面为圆形的下水管道的直径为$1\ m$,管内有少量的污水(如图),此时的水面宽$AB为0.6\ m$.
(1)求此时的水深(即阴影部分的弓形高).
(2)当水位上升到水面宽为$0.8\ m$时,求水面上升的高度.
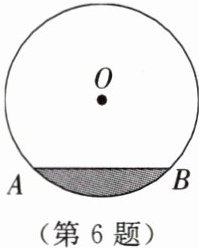
(1)求此时的水深(即阴影部分的弓形高).
(2)当水位上升到水面宽为$0.8\ m$时,求水面上升的高度.

答案:
(1) 解:设圆心为O,过O作OC⊥AB于C,交⊙O于D,连接OA。
OA=0.5m,AC=0.3m。
在Rt△OAC中,OC=√(OA²-AC²)=√(0.5²-0.3²)=0.4m。
水深CD=OD-OC=0.5-0.4=0.1m。
(2) 解:当水面宽A'B'=0.8m时,过O作OC'⊥A'B'于C',A'C'=0.4m。
OC'=√(OA²-A'C'²)=√(0.5²-0.4²)=0.3m。
当水面在圆心下方时,上升高度h1=OC-OC'=0.4-0.3=0.1m;
当水面在圆心上时,上升高度h2=OC+OC'=0.4+0.3=0.7m。
水面上升高度为0.1m或0.7m。
(1) 解:设圆心为O,过O作OC⊥AB于C,交⊙O于D,连接OA。
OA=0.5m,AC=0.3m。
在Rt△OAC中,OC=√(OA²-AC²)=√(0.5²-0.3²)=0.4m。
水深CD=OD-OC=0.5-0.4=0.1m。
(2) 解:当水面宽A'B'=0.8m时,过O作OC'⊥A'B'于C',A'C'=0.4m。
OC'=√(OA²-A'C'²)=√(0.5²-0.4²)=0.3m。
当水面在圆心下方时,上升高度h1=OC-OC'=0.4-0.3=0.1m;
当水面在圆心上时,上升高度h2=OC+OC'=0.4+0.3=0.7m。
水面上升高度为0.1m或0.7m。
查看更多完整答案,请扫码查看


