第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
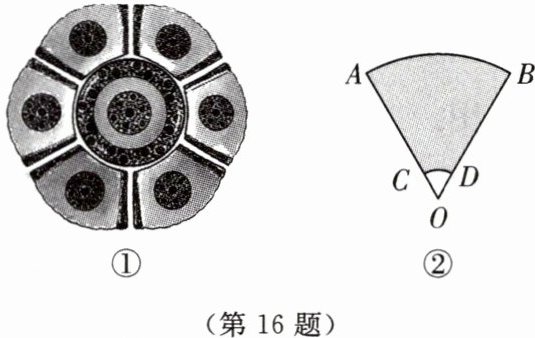
16.中国美食讲究色香味俱全,优雅的摆盘造型也会让美食锦上添花.图①中的盘子由六个造型相同的图案构成,其形状包含扇形的一部分,图②是其部分几何示意图(阴影部分为盘子盛菜区域).若$AC = BD = 12\ cm$,$OC = OD = \frac{1}{5}OA$,请你根据上述信息求图②中阴影部分的面积.

答案:
解:设 $OC = OD = x$,则 $OA = OB = 5x$。
因为 $AC = OA - OC = 5x - x = 4x = 12\ cm$,所以 $x = 3\ cm$。
故 $OA = 15\ cm$,$OC = 3\ cm$。
由于盘子由六个相同图案构成,所以 $\angle AOB = \frac{360^\circ}{6} = 60^\circ$。
阴影部分面积为扇形 $AOB$ 面积减去扇形 $COD$ 面积:
$\begin{aligned}S_{阴影}&=\frac{60^\circ}{360^\circ}\pi OA^2 - \frac{60^\circ}{360^\circ}\pi OC^2\\&=\frac{1}{6}\pi (15^2 - 3^2)\\&=\frac{1}{6}\pi (225 - 9)\\&=\frac{1}{6}\pi × 216\\&=36\pi\ cm^2\end{aligned}$
答:阴影部分面积为 $36\pi\ cm^2$。
因为 $AC = OA - OC = 5x - x = 4x = 12\ cm$,所以 $x = 3\ cm$。
故 $OA = 15\ cm$,$OC = 3\ cm$。
由于盘子由六个相同图案构成,所以 $\angle AOB = \frac{360^\circ}{6} = 60^\circ$。
阴影部分面积为扇形 $AOB$ 面积减去扇形 $COD$ 面积:
$\begin{aligned}S_{阴影}&=\frac{60^\circ}{360^\circ}\pi OA^2 - \frac{60^\circ}{360^\circ}\pi OC^2\\&=\frac{1}{6}\pi (15^2 - 3^2)\\&=\frac{1}{6}\pi (225 - 9)\\&=\frac{1}{6}\pi × 216\\&=36\pi\ cm^2\end{aligned}$
答:阴影部分面积为 $36\pi\ cm^2$。
17.在班级联谊会上进行抽奖活动,活动规则如下:将4张正面标有“龙”“蛇”“马”“羊”的纸牌(纸牌反面完全相同)洗匀后,反面朝上放在桌子上,参与者每次从中随机抽取两张纸牌.若抽到“龙”和“蛇”,即组成“笔走龙蛇”这个成语,则参与者可获得奖品.
(1)小王随机抽出一张纸牌,抽到“龙”牌的概率是______
(2)小钢决定参加游戏,请用列表法或画树状图法说明小钢获得奖品的概率.
(1)小王随机抽出一张纸牌,抽到“龙”牌的概率是______
$\frac{1}{4}$
.(2)小钢决定参加游戏,请用列表法或画树状图法说明小钢获得奖品的概率.
解:
首先,我们列出所有可能的抽取组合:
| 组合 | 第一张 | 第二张 |
| --- | --- | --- |
| 1 | 龙 | 蛇 |
| 2 | 龙 | 马 |
| 3 | 龙 | 羊 |
| 4 | 蛇 | 龙 |
| 5 | 蛇 | 马 |
| 6 | 蛇 | 羊 |
| 7 | 马 | 龙 |
| 8 | 马 | 蛇 |
| 9 | 马 | 羊 |
| 10 | 羊 | 龙 |
| 11 | 羊 | 蛇 |
| 12 | 羊 | 马 |
总共有12种可能的组合,其中抽到“龙”和“蛇”的组合有2种。
$P(获得奖品) = \frac{抽到“龙”和“蛇”的组合数}{所有可能的组合数} = \frac{2}{12} = \frac{1}{6}$
答:小钢获得奖品的概率是$\frac{1}{6}$。
首先,我们列出所有可能的抽取组合:
| 组合 | 第一张 | 第二张 |
| --- | --- | --- |
| 1 | 龙 | 蛇 |
| 2 | 龙 | 马 |
| 3 | 龙 | 羊 |
| 4 | 蛇 | 龙 |
| 5 | 蛇 | 马 |
| 6 | 蛇 | 羊 |
| 7 | 马 | 龙 |
| 8 | 马 | 蛇 |
| 9 | 马 | 羊 |
| 10 | 羊 | 龙 |
| 11 | 羊 | 蛇 |
| 12 | 羊 | 马 |
总共有12种可能的组合,其中抽到“龙”和“蛇”的组合有2种。
$P(获得奖品) = \frac{抽到“龙”和“蛇”的组合数}{所有可能的组合数} = \frac{2}{12} = \frac{1}{6}$
答:小钢获得奖品的概率是$\frac{1}{6}$。
答案:
【解析】:
本题主要考察概率的计算。
(1) 对于第一问,由于有4张纸牌,每张纸牌被抽到的概率是相等的,所以抽到“龙”牌的概率是$\frac{1}{4}$。
(2) 对于第二问,需要使用列表法或画树状图法来列出所有可能的抽取组合,并计算抽到“龙”和“蛇”的组合的概率。
【答案】:
(1) $\frac{1}{4}$
(2) 解:
首先,我们列出所有可能的抽取组合:
| 组合 | 第一张 | 第二张 |
| --- | --- | --- |
| 1 | 龙 | 蛇 |
| 2 | 龙 | 马 |
| 3 | 龙 | 羊 |
| 4 | 蛇 | 龙 |
| 5 | 蛇 | 马 |
| 6 | 蛇 | 羊 |
| 7 | 马 | 龙 |
| 8 | 马 | 蛇 |
| 9 | 马 | 羊 |
| 10 | 羊 | 龙 |
| 11 | 羊 | 蛇 |
| 12 | 羊 | 马 |
总共有12种可能的组合,其中抽到“龙”和“蛇”的组合有2种(即组合1和组合4,或者组合7和组合10等,考虑到抽取顺序,但实际成语组合不看顺序,所以只算一种情况两次,这里为简化计算,我们仍按抽取顺序算,最后做处理)。但由于成语组合不看纸牌的抽取顺序,所以实际有效的组合是2种中的任意一种,即:
$P(获得奖品) = \frac{抽到“龙”和“蛇”的组合数}{所有可能的组合数} = \frac{2}{12} = \frac{1}{6}$
由于不考虑抽取的顺序,所以有效的获奖组合只有1种情况(龙蛇或蛇龙,视为一种),但我们在上面算了两种(考虑了顺序),所以这里直接得出$\frac{2}{12}$简化为$\frac{1}{6}$也是正确的。
答:小钢获得奖品的概率是$\frac{1}{6}$。
本题主要考察概率的计算。
(1) 对于第一问,由于有4张纸牌,每张纸牌被抽到的概率是相等的,所以抽到“龙”牌的概率是$\frac{1}{4}$。
(2) 对于第二问,需要使用列表法或画树状图法来列出所有可能的抽取组合,并计算抽到“龙”和“蛇”的组合的概率。
【答案】:
(1) $\frac{1}{4}$
(2) 解:
首先,我们列出所有可能的抽取组合:
| 组合 | 第一张 | 第二张 |
| --- | --- | --- |
| 1 | 龙 | 蛇 |
| 2 | 龙 | 马 |
| 3 | 龙 | 羊 |
| 4 | 蛇 | 龙 |
| 5 | 蛇 | 马 |
| 6 | 蛇 | 羊 |
| 7 | 马 | 龙 |
| 8 | 马 | 蛇 |
| 9 | 马 | 羊 |
| 10 | 羊 | 龙 |
| 11 | 羊 | 蛇 |
| 12 | 羊 | 马 |
总共有12种可能的组合,其中抽到“龙”和“蛇”的组合有2种(即组合1和组合4,或者组合7和组合10等,考虑到抽取顺序,但实际成语组合不看顺序,所以只算一种情况两次,这里为简化计算,我们仍按抽取顺序算,最后做处理)。但由于成语组合不看纸牌的抽取顺序,所以实际有效的组合是2种中的任意一种,即:
$P(获得奖品) = \frac{抽到“龙”和“蛇”的组合数}{所有可能的组合数} = \frac{2}{12} = \frac{1}{6}$
由于不考虑抽取的顺序,所以有效的获奖组合只有1种情况(龙蛇或蛇龙,视为一种),但我们在上面算了两种(考虑了顺序),所以这里直接得出$\frac{2}{12}$简化为$\frac{1}{6}$也是正确的。
答:小钢获得奖品的概率是$\frac{1}{6}$。
查看更多完整答案,请扫码查看


