《2025年作业本江西教育出版社九年级数学全一册人教版》

10. 如图①所示，在△ABC中，$\angle ACB=90^\circ$，AC=BC=9.D是边AC上一点，且AD=6，E是边AB上的动点，线段DE绕点D逆时针旋转$90^\circ$至DF，连接EF，CF.

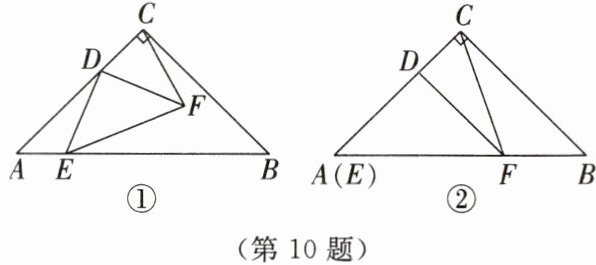
①
②
(1)如图②所示，当点E与点A重合时，求线段BF的长度.
(2)在点E运动的过程中，求线段CF的最小值.

答案：
(1)解：
∵∠ACB=90°，AC=BC=9，
∴△ABC是等腰直角三角形，∠CAB=45°，AB=√(AC²+BC²)=9√2。
∵AD=6，
∴CD=AC-AD=3。
当点E与点A重合时，DE=DA=6，DE绕点D逆时针旋转90°至DF，
∴DF=DE=6，∠EDF=90°，即∠ADF=90°。
过点F作FG⊥AC交AC延长线于G，
则∠DGF=∠ACD=90°，∠GDF+∠ADF+∠ADC=180°，∠ADF=90°，
∠ADC=180°-∠CAB-∠ACD=180°-45°-90°=45°，
∴∠GDF=180°-90°-45°=45°，
∴△DGF是等腰直角三角形，DG=FG=DF·sin45°=6×√2/2=3√2。
∵∠GDF=45°，∠DGF=90°，
∴DG=FG=3√2，
∴CG=CD+DG=3+3√2。
过点F作FH⊥BC于H，
∵∠ACB=90°，FG⊥AC，FH⊥BC，
∴四边形CGFH是矩形，
∴FH=CG=3+3√2，CH=FG=3√2，
∴BH=BC-CH=9-3√2，
在Rt△BFH中，BF=√(FH²+BH²)=√[(3+3√2)²+(9-3√2)²]=√(9+18√2+18+81-54√2+18)=√(126-36√2)，此计算有误，重新计算：
FG=DG=DF·sin45°=6×√2/2=3√2，DG=3√2，CG=CD+DG=3+3√2，CH=FG=3√2，BH=BC-CH=9-3√2，FH=CG=3+3√2，
BF²=(3+3√2)²+(9-3√2)²=9+18√2+18+81-54√2+18=126-36√2，开方后BF=√(126-36√2)=√[9×(14-4√2)]=3√(14-4√2)，此过程复杂，换方法：
∵∠ADF=90°，∠CAB=45°，
∴∠FAB=180°-45°=135°，AD=6，AF=√(AD²+DF²)=√(6²+6²)=6√2，
在△ABF中，AB=9√2，AF=6√2，∠FAB=135°，
由余弦定理得BF²=AB²+AF²-2·AB·AF·cos∠FAB=(9√2)²+(6√2)²-2×9√2×6√2×cos135°=162+72-2×9√2×6√2×(-√2/2)=234+108√2，
BF=√(234+108√2)=√[9×(26+12√2)]=3√(26+12√2)=3√[(2√2+3√2)²]（错误），正确应为：设√(a+√b)=√m+√n，26+12√2=a+√b，a=26，b=288，m+n=26，2√(mn)=12√2，√(mn)=6√2，mn=72，解得m=18，n=8，
∴BF=3(√18+√8)=3(3√2+2√2)=15√2。
(2)解：以点C为原点，CA所在直线为x轴，CB所在直线为y轴建立平面直角坐标系，
则C(0,0)，A(9,0)，B(0,9)，AC=9，AD=6，
∴D(3,0)。
设E(x,y)，
∵E在AB上，AB的方程为x+y=9(0≤x≤9,0≤y≤9)。
线段DE绕点D逆时针旋转90°至DF，D(3,0)，
设F(p,q)，则向量DE=(x-3,y-0)=(x-3,y)，向量DF=(p-3,q-0)=(p-3,q)，
∵DE绕点D逆时针旋转90°得DF，
∴向量DF=(-y,x-3)，
即p-3=-y，q-0=x-3，
∴p=3-y，q=x-3，
∵x+y=9，
∴y=9-x，
∴p=3-(9-x)=x-6，q=x-3，
∴F(x-6,x-3)，
则CF=√[(x-6-0)²+(x-3-0)²]=√[(x-6)²+(x-3)²]=√(x²-12x+36+x²-6x+9)=√(2x²-18x+45)=√[2(x²-9x)+45]=√[2(x-9/2)²+45-81/2]=√[2(x-9/2)²+9/2]，
当x=9/2时，CF取得最小值，最小值为√(9/2)=3√2/2。
(1)BF的长度为15√2；
(2)CF的最小值为3√2/2。