第103页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
15. 如图所示,在6×6的正方形网格中,点$A$,$B$,$C$均在格点上,请仅用无刻度的直尺完成以下作图。(保留作图痕迹)
(1)在图①中画一个$\triangle ADE$,使得$\triangle ADE \sim \triangle ACB$,且相似比为1:2。
(2)在图②中以$AB为直径的半圆上找一点P$,画出$\angle ABP$,使得$\angle ABP = 22.5^\circ$。

(1)在图①中画一个$\triangle ADE$,使得$\triangle ADE \sim \triangle ACB$,且相似比为1:2。
(2)在图②中以$AB为直径的半圆上找一点P$,画出$\angle ABP$,使得$\angle ABP = 22.5^\circ$。

答案:

16. 如图所示,不等臂跷跷板$AB的一端A$碰到地面时,另一端$B$到地面的高度为60 cm;当$AB的一端B$碰到地面时,另一端$A$到地面的高度为90 cm。求跷跷板$AB的支撑点O到地面的距离OH$。
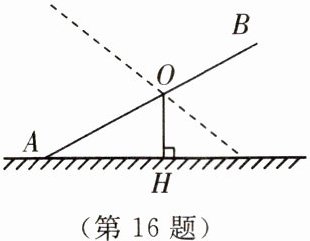

答案:
【解析】:本题可根据相似三角形的性质列出关于$OH$的方程,进而求解$OH$的长度。
设$OH = h$,$OA = a$,$OB = b$。
当一端$A$碰到地面时,另一端$B$到地面的高度为$60cm$,此时可构成相似三角形,根据相似三角形对应边成比例的性质列出方程;当一端$B$碰到地面时,另一端$A$到地面的高度为$90cm$,同样可构成相似三角形,再列出另一个方程。联立这两个方程求解$h$。
【答案】:解:设$OH = h$,$OA = a$,$OB = b$。
当$A$端碰到地面时,由相似三角形的性质可得$\frac{h}{60}=\frac{a}{a + b}$ ①;
当$B$端碰到地面时,同理可得$\frac{h}{90}=\frac{b}{a + b}$ ②;
①+②得:$\frac{h}{60}+\frac{h}{90}=\frac{a}{a + b}+\frac{b}{a + b}=1$。
通分可得:$\frac{3h}{180}+\frac{2h}{180}=1$,即$\frac{5h}{180}=1$。
解得$h = 36$。
所以跷跷板$AB$的支撑点$O$到地面的距离$OH$为$36cm$。
设$OH = h$,$OA = a$,$OB = b$。
当一端$A$碰到地面时,另一端$B$到地面的高度为$60cm$,此时可构成相似三角形,根据相似三角形对应边成比例的性质列出方程;当一端$B$碰到地面时,另一端$A$到地面的高度为$90cm$,同样可构成相似三角形,再列出另一个方程。联立这两个方程求解$h$。
【答案】:解:设$OH = h$,$OA = a$,$OB = b$。
当$A$端碰到地面时,由相似三角形的性质可得$\frac{h}{60}=\frac{a}{a + b}$ ①;
当$B$端碰到地面时,同理可得$\frac{h}{90}=\frac{b}{a + b}$ ②;
①+②得:$\frac{h}{60}+\frac{h}{90}=\frac{a}{a + b}+\frac{b}{a + b}=1$。
通分可得:$\frac{3h}{180}+\frac{2h}{180}=1$,即$\frac{5h}{180}=1$。
解得$h = 36$。
所以跷跷板$AB$的支撑点$O$到地面的距离$OH$为$36cm$。
17. 如图所示,在平面直角坐标系$xOy$中,直线$y = kx + b(k \neq 0)与双曲线y = \frac{6}{x}相交于点A(m,6)和点B(-3,n)$,直线$AB与y轴交于点C$。
(1)求直线$AB$的函数解析式。
(2)求$\frac{AC}{CB}$的值。
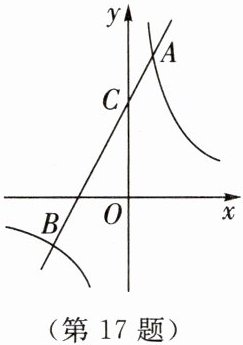
(1)求直线$AB$的函数解析式。
(2)求$\frac{AC}{CB}$的值。

答案:
(1)解:
∵点A(m,6)在双曲线$y=\frac{6}{x}$上,
∴$6=\frac{6}{m}$,解得$m=1$,
∴A(1,6)。
∵点B(-3,n)在双曲线$y=\frac{6}{x}$上,
∴$n=\frac{6}{-3}=-2$,
∴B(-3,-2)。
将A(1,6),B(-3,-2)代入$y=kx+b$,
得$\begin{cases}k+b=6\\-3k+b=-2\end{cases}$,
解得$\begin{cases}k=2\\b=4\end{cases}$,
∴直线AB的函数解析式为$y=2x+4$。
(2)解:在$y=2x+4$中,令$x=0$,得$y=4$,
∴C(0,4)。
过A作AD⊥y轴于D,过B作BE⊥y轴于E,
则AD=1,BE=3,∠ADC=∠BEC=90°。
∵∠ACD=∠BCE,
∴△ACD∽△BCE,
∴$\frac{AC}{CB}=\frac{AD}{BE}=\frac{1}{3}$。
(1)解:
∵点A(m,6)在双曲线$y=\frac{6}{x}$上,
∴$6=\frac{6}{m}$,解得$m=1$,
∴A(1,6)。
∵点B(-3,n)在双曲线$y=\frac{6}{x}$上,
∴$n=\frac{6}{-3}=-2$,
∴B(-3,-2)。
将A(1,6),B(-3,-2)代入$y=kx+b$,
得$\begin{cases}k+b=6\\-3k+b=-2\end{cases}$,
解得$\begin{cases}k=2\\b=4\end{cases}$,
∴直线AB的函数解析式为$y=2x+4$。
(2)解:在$y=2x+4$中,令$x=0$,得$y=4$,
∴C(0,4)。
过A作AD⊥y轴于D,过B作BE⊥y轴于E,
则AD=1,BE=3,∠ADC=∠BEC=90°。
∵∠ACD=∠BCE,
∴△ACD∽△BCE,
∴$\frac{AC}{CB}=\frac{AD}{BE}=\frac{1}{3}$。
查看更多完整答案,请扫码查看


