《2025年作业本江西教育出版社九年级数学全一册人教版》

1. 已知二次函数 $ y= -2x^2 - 4x + 5 $,当 $ x $ 取任意实数时,$ y $ 的最大值是7；当 $ -3 \leq x \leq -2 $ 时,$ y $ 的最小值为-1,最大值为5；当 $ -2 \leq x \leq 1 $ 时,$ y $ 的最小值为-1,最大值为7.

答案： 解：
1. $y=-2x^2-4x+5=-2(x+1)^2+7$，

∵$-2＜0$，
∴当$x=-1$时，$y$有最大值$7$。
2. 当$-3 \leq x \leq -2$时，
对称轴$x=-1$在区间右侧，$y$随$x$增大而增大，
$x=-3$时，$y=-2(-3)^2-4(-3)+5=-18+12+5=-1$；
$x=-2$时，$y=-2(-2)^2-4(-2)+5=-8+8+5=5$，

∴最小值为$-1$，最大值为$5$。
3. 当$-2 \leq x \leq 1$时，
对称轴$x=-1$在区间内，$x=-1$时，$y=7$；
$x=1$时，$y=-2(1)^2-4(1)+5=-2-4+5=-1$，

∴最小值为$-1$，最大值为$7$。
答案：$7$；$-1$，$5$；$-1$，$7$

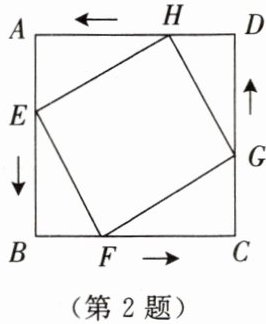
2. 如图所示,在边长为 6 cm 的正方形 $ ABCD $ 中,点 $ E,F,G,H $ 分别从点 $ A,B,C,D $ 同时出发,均以 1 cm/s 的速度向点 $ B,C,D,A $ 匀速运动.当点 $ E $ 到达点 $ B $ 时,四个点同时停止运动.在运动过程中,当运动时间为3s 时,四边形 $ EFGH $ 的面积最小,其最小值是18$ cm^2 $.

答案： 【解析】：
本题可先设出运动时间，再根据正方形的性质和勾股定理表示出四边形$EFGH$的面积，最后根据二次函数的性质求出面积最小时的运动时间。
设运动时间为$t$秒（$0\leq t\leq6$），则$AE = t$厘米，$EB=(6 - t)$厘米，$BF = t$厘米，$FC=(6 - t)$厘米，$CG = t$厘米，$GD=(6 - t)$厘米，$DH = t$厘米，$HA=(6 - t)$厘米。
在$Rt\triangle AEH$中，根据勾股定理可得$EH^{2}=AE^{2}+AH^{2}=t^{2}+(6 - t)^{2}$。
同理，在$Rt\triangle BEF$中，$EF^{2}=BE^{2}+BF^{2}=(6 - t)^{2}+t^{2}$；在$Rt\triangle CFG$中，$FG^{2}=CF^{2}+CG^{2}=(6 - t)^{2}+t^{2}$；在$Rt\triangle DGH$中，$GH^{2}=DG^{2}+DH^{2}=(6 - t)^{2}+t^{2}$。
所以四边形$EFGH$的面积$S = S_{正方形ABCD}-(S_{\triangle AEH}+S_{\triangle BEF}+S_{\triangle CFG}+S_{\triangle DGH})$。
$S_{\triangle AEH}=\frac{1}{2}× AE× AH=\frac{1}{2}t(6 - t)$，同理$S_{\triangle BEF}=S_{\triangle CFG}=S_{\triangle DGH}=\frac{1}{2}t(6 - t)$。
则$S = 36 - 4×\frac{1}{2}t(6 - t)=36 - 2t(6 - t)=36 - 12t + 2t^{2}=2t^{2}-12t + 36$。
对于二次函数$y = 2t^{2}-12t + 36$，其中$a = 2\gt0$，函数图象开口向上，对称轴为$t = -\frac{b}{2a}=-\frac{-12}{2×2}= 3$。
所以当$t = 3$时，$S$有最小值，$S_{min}=2×3^{2}-12×3 + 36=18$。
【答案】：
$3$；$18$

3. 如图所示,某农场要建一个矩形养鸡场,养鸡场的一边靠墙,另外三边用木栅栏围成.已知墙长 25 m,木栅栏长 47 m,在与墙垂直的一边留出 1 m 宽的出入口(另选材料建出入门).求养鸡场面积的最大值.

答案： 【解析】：本题考查二次函数解决实际问题最大值的知识点。
首先设与墙垂直的边长为$x$米，因为木栅栏总长是$47$米，且在与墙垂直的一边留出$1$米宽的出入口（另选材料建出入门），所以与墙平行的边长为$(47 + 1 - 2x)$米，也就是$(48 - 2x)$米。
然后根据矩形面积公式$S = 长×宽$，可得到面积$S$与$x$的函数关系式$S = x(48 - 2x)$，将其化为顶点式来求面积的最大值，同时要考虑墙长$25$米这个限制条件对$x$取值范围的影响。
【答案】：解：设与墙垂直的边长为$x$米，则与墙平行的边长为$(47 + 1 - 2x)=(48 - 2x)$米。
养鸡场面积$S = x(48 - 2x)=-2x^{2} + 48x$。
因为墙长$25$米，所以$0＜48 - 2x\leqslant25$，
解不等式$48 - 2x＞0$，得$x＜24$；
解不等式$48 - 2x\leqslant25$，
移项可得$-2x\leqslant25 - 48$，即$-2x\leqslant - 23$，
两边同时除以$-2$，不等号变向，得$x\geqslant11.5$。
所以$11.5\leqslant x＜24$。
对于二次函数$S = - 2x^{2} + 48x$，其中$a=-2$，$b = 48$，根据二次函数顶点坐标公式$x=-\frac{b}{2a}$，
可得$x = -\frac{48}{2×(-2)} = 12$。
因为$a=-2＜0$，所以二次函数图象开口向下，在对称轴$x = 12$处取得最大值。
把$x = 12$代入$S = - 2x^{2} + 48x$，
$S=-2×12^{2}+48×12$
$=-2×144 + 576$
$=-288+576$
$= 288$（平方米）
答：养鸡场面积的最大值为$288$平方米。

4. 如图所示,等腰直角三角形 $ ABC $ 以 2 cm/s 的速度沿直线 $ m $ 匀速向正方形 $ DEFG $ 移动,直到 $ AB $ 与 $ EF $ 重合.设移动 $ x $ s 时,三角形与正方形重合部分的面积为 $ y \, cm^2 $.

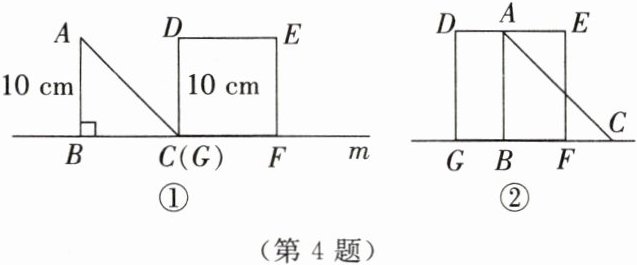
(1)当 $ x= 2,7 $ 时,$ y $ 的值分别为多少？
(2)求从开始移动到AB与EF重合时,y与x的关系式,并求出x的取值范围

答案： $(1)$ 计算当$x = 2$和$x = 7$时$y$的值
- 当$x = 2$时：
已知三角形移动速度为$2cm/s$，根据路程$s=vt$（$v$是速度，$t$是时间），则移动的距离$s = 2×2=4cm$。
因为$\triangle ABC$是等腰直角三角形，重合部分也是等腰直角三角形，根据等腰直角三角形面积公式$S=\frac{1}{2}a^{2}$（$a$为直角边），此时直角边$a = 4cm$，所以$y=\frac{1}{2}×4^{2}=8cm^{2}$。
当$x = 7$时：
移动的距离$s=2×7 = 14cm$，那么未重合部分的直角边为$10-(14 - 10)=6cm$。
此时重合部分面积$y=\frac{1}{2}×10^{2}-\frac{1}{2}×6^{2}=50 - 18=32cm^{2}$。
$(2)$ 求$y$与$x$之间的关系式及$x$的取值范围
当$0\leqslant x\leqslant5$时**：
移动距离为$2x$，重合部分是等腰直角三角形，根据等腰直角三角形面积公式$y=\frac{1}{2}(2x)^{2}=2x^{2}$。
当$5\lt x\leqslant10$时**：
移动距离为$2x$，未重合部分的直角边为$2x - 10$，根据$y=\frac{1}{2}×10^{2}-\frac{1}{2}(2x - 10)^{2}$，展开可得：
$\begin{aligned}y&=50-\frac{1}{2}(4x^{2}-40x + 100)\\&=50-(2x^{2}-20x + 50)\\&=- 2x^{2}+20x\end{aligned}$
从开始移动到$AB$与$EF$重合，移动的总距离为$10×2 = 20cm$，根据$t=\frac{s}{v}$，可得$x$的取值范围是$0\leqslant x\leqslant10$。
所以$y$与$x$之间的关系式为$y=\begin{cases}2x^{2}&(0\leqslant x\leqslant5)\\-2x^{2}+20x&(5\lt x\leqslant10)\end{cases}$，$x$的取值范围是$0\leqslant x\leqslant10$。
综上，$(1)$ 当$x = 2$时，$y = 8cm^{2}$；当$x = 7$时，$y = 32cm^{2}$；$(2)$ $y=\begin{cases}2x^{2}&(0\leqslant x\leqslant5)\\-2x^{2}+20x&(5\lt x\leqslant10)\end{cases}$，$x$取值范围是$\boldsymbol{0\leqslant x\leqslant10}$。