《2025年作业本江西教育出版社九年级数学全一册人教版》

1. 抛物线 $ y= -x^2,y= x^2-3,y= -\frac{1}{2}x^2+2 $ 共有的特征是(A)
A.对称轴是 y 轴
B.开口向上
C.都有最低点
D.y 随 x 的增大而减小

答案： 【解析】：
本题主要考察二次函数的图像与性质。
对于给定的三个函数：
$y = -x^2$：
这是一个开口向下的抛物线，因为二次项系数$a=-1＜0$，对称轴是y轴，即$x=0$，有最高点，无最低点。
$y = x^2 - 3$：
这是一个开口向上的抛物线，因为二次项系数$a=1＞0$，对称轴是y轴，即$x=0$，有最低点，无最高点。
$y = -\frac{1}{2}x^2 + 2$：
这是一个开口向下的抛物线，因为二次项系数$a=-\frac{1}{2}＜0$，对称轴是y轴，即$x=0$，有最高点，无最低点。
A. 对于这三个函数，由于它们都是二次函数且没有x的一次项，所以它们的对称轴都是y轴，即$x=0$。此选项正确。
B. $y = -x^2$ 和 $y = -\frac{1}{2}x^2 + 2$ 的开口方向是向下的，而 $y = x^2 - 3$ 的开口方向是向上的。所以此选项错误。
C. $y = -x^2$ 和 $y = -\frac{1}{2}x^2 + 2$ 有最高点，无最低点，而 $y = x^2 - 3$ 有最低点，无最高点。所以此选项错误。
D. 对于开口向上的抛物线，当x在对称轴左侧时，y随x的增大而减小；当x在对称轴右侧时，y随x的增大而增大。对于开口向下的抛物线，情况相反。所以此选项错误。
【答案】：A

2. 关于函数 $ y= -(x+3)^2-2 $ 的图象,下列叙述正确的是(B)
A.开口向上
B.图象在 x 轴下方
C.与 y 轴的交点为(0,-2)
D.顶点坐标为(3,-2)

答案： 【解析】：
首先，分析函数$y = -(x + 3)^{2} - 2$的基本性质。
这是一个开口向下的抛物线，因为二次项的系数是负数（-1）。
其次，找出该函数的顶点坐标和与坐标轴的交点。
顶点坐标可以通过公式直接得出，为$(-3, -2)$。
与$y$轴的交点可以通过将$x=0$代入原函数得出，即$(0, - (0 + 3)^{2} - 2) = (0, -11)$。
接着，判断图象的位置。
由于抛物线开口向下，并且顶点的$y$坐标为$-2$（小于$0$），因此整个图象都在$x$轴下方。
最后，根据以上分析，逐一判断选项：
A. 开口向上：错误，因为二次项系数是负数，所以开口向下。
B. 图象在$x$轴下方：正确，因为抛物线开口向下，并且顶点的$y$坐标小于$0$。
C. 与$y$轴的交点为$(0,-2)$：错误，实际交点为$(0, -11)$。
D. 顶点坐标为$(3,-2)$：错误，实际顶点坐标为$(-3, -2)$。
【答案】：B

3. 如果 $ y= (m-2)x^{|m|}+5 $ 是 y 关于 x 的二次函数,那么 m 的值为$-2$.

答案： 解：因为$y = (m - 2)x^{|m|} + 5$是二次函数，所以$\begin{cases} |m| = 2 \\ m - 2 \neq 0 \end{cases}$
由$|m| = 2$得$m = \pm 2$，由$m - 2 \neq 0$得$m \neq 2$，所以$m = -2$
答案：$-2$

4. 已知二次函数 $ y= ax^2+bx+c $ 的图象如图所示,有以下结论：
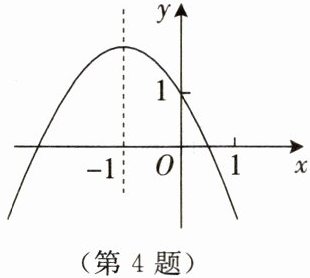
①$ a-b+c＞0 $；②$ 4a-2b+c＜0 $；③$ 3a+c＜0 $；④$ a-b＞m(am+b) $(m≠-1且m为实数). 其中正确的是______(填序号).

①③④

答案： 【解析】：本题主要考查二次函数图象与系数的关系以及二次函数与不等式的关系。
对于①：
由图象可知，当$x=-1$时，$y＞0$。
将$x=-1$代入二次函数$y=ax^2+bx+c$，可得$y=a×(-1)^2+b×(-1)+c=a-b+c$，所以$a-b+c＞0$，故①正确。
对于②：
由图象可知，二次函数的对称轴为$x=-1$，根据二次函数的对称性，图象关于对称轴对称，那么$x=-2$时的函数值与$x=0$时的函数值相等。
当$x=0$时，$y＞0$，所以当$x=-2$时，$y=4a-2b+c＞0$，故②错误。
对于③：
由对称轴$x=-1$，根据对称轴公式$x=-\frac{b}{2a}$，可得$-\frac{b}{2a}=-1$，即$b=2a$。
由①知$a-b+c＞0$，把$b=2a$代入$a-b+c＞0$中，得到$a-2a+c＞0$，即$-a+c＞0$，也就是$c＞a$。
当$x=1$时，$y=a+b+c＜0$，把$b=2a$代入$a+b+c＜0$中，得到$a+2a+c＜0$，即$3a+c＜0$，故③正确。
对于④：
因为对称轴为$x=-1$，所以当$x=-1$时，$y$有最大值$a-b+c$。
当$x=m$（$m\neq-1$且$m$为实数）时，$y=am^2+bm+c$。
由于$x=-1$时$y$最大，所以$a-b+c＞am^2+bm+c$，两边同时减去$c$，得到$a-b＞am^2+bm$，即$a-b＞m(am+b)$（$m\neq-1$且$m$为实数），故④正确。
综上，正确的是①③④。
【答案】：①③④

5. 一个二次函数图象上部分点的横坐标x、纵坐标y的对应值如下表所示：
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| y | … | 5 | 0 | -3 | -4 | -3 | m | … |
(1)m的值是______.
(2)求此二次函数的解析式.
(3)在图中画出这个二次函数的图象.
(4)当 $ y\geq5 $ 时,x的取值范围是______.
(5)当 $-4＜x＜1$ 时,y的取值范围是______.

答案：
【解析】：
（1）观察表格可知，当$x=-2$和$x = 0$时，$y$的值都为$-3$，根据二次函数图象的对称性，可知二次函数图象的对称轴为$x=\frac{-2 + 0}{2}=-1$。
点$(-4,5)$关于对称轴$x = - 1$的对称点的横坐标为$2×(-1)-(-4)=2$，因为二次函数图象关于对称轴对称，所以$m$的值与$x=-4$时$y$的值相等，即$m = 0$。
（2）已知二次函数图象的对称轴为$x=-1$，所以设二次函数的解析式为$y=a(x + 1)^{2}+k$（$a\neq0$）。
把$(-1,-4)$和$(0,-3)$代入解析式可得：
$\begin{cases}a(-1 + 1)^{2}+k=-4,\\a(0 + 1)^{2}+k=-3.\end{cases}$
即$\begin{cases}k=-4,\\a + k=-3.\end{cases}$
将$k = - 4$代入$a + k=-3$，可得$a-4=-3$，解得$a = 1$。
所以二次函数的解析式为$y=(x + 1)^{2}-4$，展开得$y=x^{2}+2x - 3$。
（3）图略（按照列表、描点、连线的步骤画图，以表格中的点为基础，再适当选取一些点，用平滑曲线连接）。
（4）已知当$x=-4$时，$y = 5$，由二次函数图象的对称性，对称轴为$x=-1$，则点$(-4,5)$关于对称轴$x=-1$的对称点为$(2,5)$。
因为二次函数$y=x^{2}+2x - 3$中$a = 1＞0$，图象开口向上，所以当$y\geq5$时，$x$的取值范围是$x\leq - 4$或$x\geq2$。
（5）由表格可知，当$x=-1$时，$y$有最小值$-4$。
当$x=-4$时，$y = 5$，当$x = 1$时，$y=1^{2}+2×1 - 3=0$。
因为二次函数图象开口向上，在$-4＜x＜1$这个区间内，$y$的最小值是$-4$，最大值在$x=-4$处取得（但$x=-4$不在此区间），当$x$趋近于$-4$时$y$趋近于$5$，$y$随$x$的增大而增大（$x＞-1$时），所以$y$的取值范围是$-4\leq y＜5$。
【答案】：
(1)$0$
(2)$y=x^{2}+2x - 3$
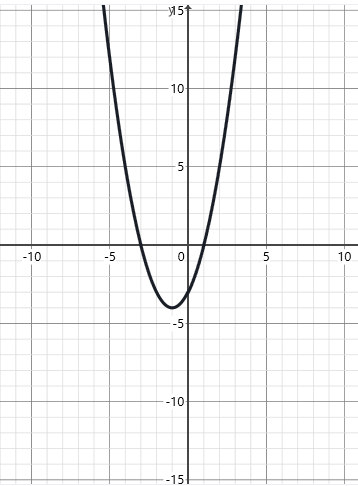
(3)
(4)$x\leq - 4$或$x\geq2$
(5)$-4\leq y＜5$