《2025年作业本江西教育出版社九年级数学全一册人教版》

1. 参加某次联欢会的任意两个人都握了一次手,所有人共握手 45 次. 若设有x人参加联欢会,则根据题意可列方程为$\frac{1}{2}x(x - 1) = 45$（或$x(x - 1) = 90$）.

答案： 【解析】：
这是一道涉及一元二次方程的实际问题，主要考察的是从实际问题中抽象出一元二次方程的能力。
题目描述了参加联欢会的任意两个人都握了一次手，所有人共握手45次。
设有x人参加联欢会，我们需要找出根据这个设定能列出怎样的一元二次方程。
每个人都需要和其他$x-1$个人握手，所以x个人总共需要握$x(x-1)$次手。
但这样每次握手都被计算了两次（A和B握手，既算作A握了B的手，也算作B握了A的手），所以需要除以2，即$\frac{1}{2}x(x-1)$。
根据题意，这个数应该等于45，所以我们有方程：
$\frac{1}{2}x(x - 1) = 45$。
进一步整理，也可以得到：
$x(x - 1) = 90$。
【答案】：
$x(x - 1) = 90$（或 $\frac{1}{2}x(x - 1) = 45$）。

2. 若两个相邻的偶数的积为 48,则这两个偶数分别为-8 和 -6 或 6 和 8.

答案： 解：设较小的偶数为$x$，则较大的偶数为$x + 2$。
根据题意，得$x(x + 2) = 48$。
整理，得$x^2 + 2x - 48 = 0$。
因式分解，得$(x + 8)(x - 6) = 0$。
解得$x_1 = -8$，$x_2 = 6$。
当$x = -8$时，$x + 2 = -6$；当$x = 6$时，$x + 2 = 8$。
这两个偶数分别为$-8$和$-6$或$6$和$8$。

3. 在毕业晚会上,某班每名同学向本班的其他同学赠送 1 份自己制作的小礼物. 全班制作的小礼物共有 1260 份,设该班共有x名学生,则可列方程为x(x - 1) = 1260.

答案： 解：设该班共有$x$名学生，每名同学向本班的其他同学赠送$1$份礼物，则每名同学赠送$(x - 1)$份礼物，全班共赠送$x(x - 1)$份礼物。
已知全班制作的小礼物共有$1260$份，所以可列方程为$x(x - 1) = 1260$。
故答案为：$x(x - 1) = 1260$

4. 女子冰壶比赛有若干支队伍参加了单循环赛,单循环赛共进行了 45 场,那么共有10支队伍参加比赛.

答案： 【解析】：
本题考查的是单循环赛制下的比赛场数计算问题，需要用到一元二次方程的知识点。
在单循环赛制中，每两支队伍都会进行一场比赛。
假设有$x$支队伍参加比赛，那么第一支队伍会和其他$x-1$支队伍进行比赛，第二支队伍会和其他$x-2$支队伍进行比赛（因为已经和第一支队伍比赛过了），以此类推，最后一支队伍不需要再和其他队伍比赛，因为已经都比赛过了。
所以总的比赛场数为：
$1 + 2 + 3 + \ldots + (x-1)$
这是一个等差数列的和，其和公式为：
$S = \frac{x(x-1)}{2}$
根据题目，这个和等于45，所以我们有方程：
$\frac{x(x-1)}{2} = 45$
$x(x-1) = 90$
$x^2 - x - 90 = 0$
解这个一元二次方程，我们得到两个解，但需要根据实际情况选择正数解。
【答案】：
解：设参加比赛的队伍数为$x$支。
根据单循环赛制，比赛场数为$\frac{x(x-1)}{2}$，根据题意有方程：
$\frac{x(x-1)}{2} = 45$
$x^2 - x - 90 = 0$
通过求解一元二次方程，我们得到：
$x_{1} = 10, x_{2} = -9$
由于队伍数不能为负，所以$x_{2} = -9$不符合实际情况，舍去。
所以，参加比赛的队伍数为$x = 10$。
故答案为：10。

5. 为了推广“乡村篮球冠军杯”,某志愿者用网络转发的形式对推广活动进行宣传. 他将活动方案发表在自己的公众号上,再邀请n个好友转发,每个好友转发后,又邀请互不相同的n个好友转发. 以此类推,经过两轮转发推广后,共有 421 人参与了推广活动,求n的值.

答案： 【解析】：
本题主要考察一元二次方程在实际问题中的应用。
根据题意，志愿者本人为1人，第一轮转发后有n人参与，第二轮转发后，每个第一轮的好友都邀请了n个互不相同的好友，所以第二轮有$n^2$人参与。
因此，总人数为志愿者本人加上第一轮和第二轮的转发人数，即$1 + n + n^2$。
根据题意，这个总人数等于421，所以我们可以得到方程：
$1 + n + n^2 = 421$
整理得：
$n^2 + n - 420 = 0$
接下来，我们解这个一元二次方程。
首先，计算判别式$\Delta$：
$\Delta = b^2 - 4ac = 1^2 - 4 × 1 × (-420) = 1 + 1680 = 1681$
由于$\Delta ＞ 0$，方程有两个不相等的实根。
然后，利用求根公式求解方程：
$n = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-1 \pm \sqrt{1681}}{2} = \frac{-1 \pm 41}{2}$
解得：
$n_1 = \frac{40}{2} = 20$
$n_2 = \frac{-42}{2} = -21$
由于n表示人数，所以n不能为负，故$n = -21$不符合题意，舍去。
所以，n的值为20。
【答案】：
$n = 20$

6. 某班有 48 名同学,如果每两名同学之间都通一次电话,那么全班同学共通多少次电话呢？我们可以用下面的模型来解决问题：用点$A_{1},A_{2},A_{3},…,A_{48}$分别表示第 1 名同学、第 2 名同学、第 3 名同学……第 48 名同学,把该班级人数x与通电话次数y之间的关系用图示模型表示.

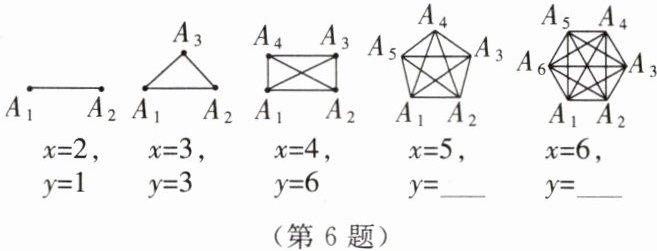
$A_{1}A_{2}$ $x= 2$,$y= 1$
$A_{1}A_{2}A_{3}$ $x= 3$,$y= 3$
$A_{1}A_{2}A_{3}A_{4}$ $x= 4$,$y= 6$
$A_{1}A_{2}A_{3}A_{4}A_{5}$ $x= 5$,$y= $10
$A_{1}A_{2}A_{3}A_{4}A_{5}A_{6}$ $x= 6$,$y= $15
(1)上面第四个图中y的值为10,第五个图中y的值为15.
(2)通过探索发现,通电话次数y与该班级人数x之间的关系为$y=\frac{1}{2}x(x - 1)$,当$x= 48$时,对应的$y= $1128.
(3)若九年级 1 班全体女生相互之间共通话 190 次,则该班共有多少名女生？
该班共有20名女生。

答案： 1. （1）
对于$x = 5$时：
从$A_1$出发，可以和$A_2$，$A_3$，$A_4$，$A_5$通电话，共$4$次；从$A_2$出发（除去与$A_1$已通的），可以和$A_3$，$A_4$，$A_5$通电话，共$3$次；从$A_3$出发（除去与$A_1$，$A_2$已通的），可以和$A_4$，$A_5$通电话，共$2$次；从$A_4$出发（除去与$A_1$，$A_2$，$A_3$已通的），可以和$A_5$通电话，共$1$次。
所以$y=4 + 3+2 + 1=\frac{4×(4 + 1)}{2}=10$。
对于$x = 6$时：
从$A_1$出发，可以和$A_2$，$A_3$，$A_4$，$A_5$，$A_6$通电话，共$5$次；从$A_2$出发（除去与$A_1$已通的），可以和$A_3$，$A_4$，$A_5$，$A_6$通电话，共$4$次；从$A_3$出发（除去与$A_1$，$A_2$已通的），可以和$A_4$，$A_5$，$A_6$通电话，共$3$次；从$A_4$出发（除去与$A_1$，$A_2$，$A_3$已通的），可以和$A_5$，$A_6$通电话，共$2$次；从$A_5$出发（除去与$A_1$，$A_2$，$A_3$，$A_4$已通的），可以和$A_6$通电话，共$1$次。
所以$y=5 + 4+3 + 2+1=\frac{5×(5 + 1)}{2}=15$。
故答案依次为$10$；$15$。
2. （2）
通过前面的计算，我们发现$y=\frac{(x - 1)x}{2}$（$x\geq2$且$x$为整数）。
当$x = 48$时，$y=\frac{48×(48 - 1)}{2}=\frac{48×47}{2}=1128$。
故答案依次为$y=\frac{x(x - 1)}{2}$（$x\geq2$且$x$为整数）；$1128$。
3. （3）
解：设该班有$x$名女生，根据$y=\frac{x(x - 1)}{2}$，已知$y = 190$，则$\frac{x(x - 1)}{2}=190$。
方程两边同时乘以$2$得：$x(x - 1)=380$，即$x^{2}-x - 380=0$。
对于一元二次方程$ax^{2}+bx + c = 0$（这里$a = 1$，$b=-1$，$c = - 380$），根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$，先计算$\Delta=b^{2}-4ac=(-1)^{2}-4×1×(-380)=1 + 1520 = 1521$。
则$x=\frac{1\pm\sqrt{1521}}{2}=\frac{1\pm39}{2}$。
解得$x_1=\frac{1 + 39}{2}=20$，$x_2=\frac{1-39}{2}=-19$（人数不能为负数，舍去）。
所以该班共有$20$名女生。