《2025年作业本江西教育出版社九年级数学全一册人教版》

1. 已知⊙O的半径为5,若⊙O与直线AB相离,则点O到直线AB的距离d的取值范围是d＞5.

答案： 【解析】：
本题考查的是直线与圆的位置关系。
已知⊙O的半径为5。
根据直线与圆的位置关系，若直线与圆相离，则圆心到直线的距离大于圆的半径。
设点O到直线AB的距离为d，由于⊙O与直线AB相离，所以有 $d ＞ 5$。
【答案】：
$d ＞ 5$

2. 若⊙O的直径为12 cm,圆心O到直线l的距离为5 cm,则直线l与⊙O的公共点个数为2.

答案： 解：
∵⊙O的直径为12 cm，
∴⊙O的半径r = 6 cm。
∵圆心O到直线l的距离d = 5 cm，
∵d = 5 cm ＜ r = 6 cm，
∴直线l与⊙O相交，
∴直线l与⊙O的公共点个数为2。
答案：2

3. 在Rt△ABC中,∠C= 90°,∠B= 30°,BC= 4,以点C为圆心,半径为2的圆与AB的位置关系是相切.

答案： 1. 首先求点$C$到$AB$的距离$d$：
在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$\angle B = 30^{\circ}$，$BC = 4$。
根据三角函数关系，$\sin B=\frac{AC}{AB}$，$\cos B=\frac{BC}{AB}$，且$\tan B=\frac{AC}{BC}$。
因为$\tan B=\tan30^{\circ}=\frac{AC}{BC}$，$BC = 4$，所以$AC = BC\tan30^{\circ}=4×\frac{\sqrt{3}}{3}=\frac{4\sqrt{3}}{3}$。
再根据三角形面积公式$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot d$（$d$为$C$到$AB$的距离）。
由勾股定理$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{(\frac{4\sqrt{3}}{3})^{2}+4^{2}}=\sqrt{\frac{16}{3}+16}=\sqrt{\frac{16 + 48}{3}}=\frac{8\sqrt{3}}{3}$。
又$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}×\frac{4\sqrt{3}}{3}×4=\frac{8\sqrt{3}}{3}$，且$S_{\triangle ABC}=\frac{1}{2}AB\cdot d$，把$AB = \frac{8\sqrt{3}}{3}$代入$\frac{1}{2}AB\cdot d=\frac{8\sqrt{3}}{3}$，即$\frac{1}{2}×\frac{8\sqrt{3}}{3}\cdot d=\frac{8\sqrt{3}}{3}$，解得$d = 2$。
2. 然后根据直线与圆的位置关系判断：
已知圆的半径$r = 2$，点$C$到直线$AB$的距离$d = 2$。
当$d=r$时，直线与圆相切。
故答案为：相切。

4. 在平面直角坐标系内,若以点P(-1,0)为圆心、$\sqrt{5}$为半径作圆,则该圆与y轴的交点坐标是$(0, 2)$，$(0, -2)$.

答案： 【解析】：
本题主要考查了直线与圆的位置关系中的相切，以及勾股定理的应用。
首先，确定圆心$P(-1,0)$到$y$轴的距离。由于$y$轴的方程是$x=0$，所以圆心$P$到$y$轴的距离为$|-1|=1$。
已知圆的半径为$\sqrt{5}$，利用勾股定理计算圆与$y$轴的交点坐标。
设交点坐标为$(0, y)$，则$OP$与交点与圆心$P$的连线（即半径）和$y$轴构成一个直角三角形。
其中，直角边之一为圆心到$y$轴的距离1，另一直角边为$y$的绝对值，斜边为圆的半径$\sqrt{5}$。
根据勾股定理，有：
$1^2 + y^2 = (\sqrt{5})^2$，
$1 + y^2 = 5$，
$y^2 = 4$，
解得$y = \pm 2$。
因此，该圆与$y$轴的交点坐标是$(0, 2)$和$(0, -2)$。
【答案】：
$(0, 2)$，$(0, -2)$。

5. 若⊙O的半径是5,圆心O到直线AB的距离为2,则⊙O上有且只有3个点到直线AB的距离为3.

答案： 解：
过圆心O作直线AB的垂线，垂足为C，则OC=2。
在垂线上取点D，使CD=3，分两种情况：
1. 点D在直线AB上方：OD=OC+CD=2+3=5，此时点D在⊙O上；
2. 点D在直线AB下方：OD=|OC-CD|=|2-3|=1，此时以D为圆心、3为半径的直线与⊙O相交，有2个交点。
综上，⊙O上到直线AB距离为3的点共有3个。
答案：3

6. 如图所示,已知∠APB= 30°,OP= 3 cm,⊙O的半径为1 cm. 若圆心O沿着BP的方向在直线BP上移动.

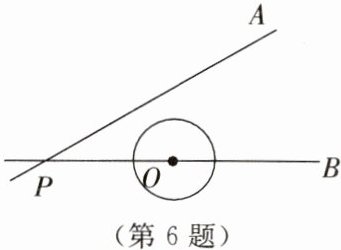
(1)当圆心O移动的距离为1 cm时,请判断直线PA与⊙O的位置关系,并说明理由.
(2)若圆心O的移动距离是d,当直线PA与⊙O相交时,求d的取值范围.

答案：
(1)解：直线PA与⊙O相切。理由如下：
过点O作OC⊥PA于点C。
当圆心O沿BP方向移动1cm时，OP' = 3 - 1 = 2cm（设移动后圆心为O'）。
在Rt△O'CP中，∠O'PC = 30°，O'P = 2cm，
则O'C = O'P·sin30° = 2×(1/2) = 1cm。
∵⊙O半径为1cm，
∴O'C等于半径，故直线PA与⊙O相切。
(2)解：设圆心移动距离为d，分两种情况：
①圆心沿BP方向向P移动（O在P、B之间）：OP' = 3 - d，
圆心到PA距离O'C = (3 - d)·sin30° = (3 - d)/2。
当直线PA与⊙O相交时，(3 - d)/2 ＜ 1，解得d ＞ 1。
又
∵O在BP上，
∴d ≤ 3。
②圆心沿BP方向远离P移动（O在B右侧）：OP' = 3 + d，
圆心到PA距离O'C = (3 + d)·sin30° = (3 + d)/2。
当直线PA与⊙O相交时，(3 + d)/2 ＜ 1，解得d ＜ -1（不合题意，舍去）。
综上，d的取值范围是1 ＜ d ≤ 3。

7. 在Rt△ABC中,∠C= 90°,BC= 4 cm,AC= 3 cm. 如图所示,以点C为圆心,r为半径作⊙C.

(1)若直线AB与⊙C没有公共点,求r的取值范围.
(2)若边AB与⊙C有两个公共点,求r的取值范围.
(3)若边AB与⊙C只有一个公共点,求r的取值范围.

答案： 【解析】：本题主要考查直线与圆的位置关系，可根据直线与圆的位置关系的判定方法，结合勾股定理求出斜边$AB$上的高，进而确定$r$的取值范围。
步骤一：求出斜边$AB$的长度
在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$BC = 4cm$，$AC = 3cm$，根据勾股定理$AB^{2}=AC^{2}+BC^{2}$，可得：
$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}} = 5cm$
步骤二：求出斜边$AB$上的高$CD$的长度
根据三角形面积公式$S=\frac{1}{2}ah$（$a$为底，$h$为高），可得$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$，即$\frac{1}{2}×3×4=\frac{1}{2}×5× CD$，解得$CD = \frac{12}{5}= 2.4cm$。
步骤三：分别求解各小题$r$的取值范围
（1）若直线$AB$与$\odot C$没有公共点
当直线与圆没有公共点时，直线与圆相离，此时圆心到直线的距离$d\gt r$（$d$为圆心$C$到直线$AB$的距离，即$CD$的长度）。
已知$CD = 2.4cm$，所以$r\lt 2.4cm$，又因为$r\gt0$，故$0\lt r\lt 2.4$。
（2）若边$AB$与$\odot C$有两个公共点
当直线与圆有两个公共点时，直线与圆相交，此时圆心到直线的距离$d\lt r$，且$r\lt AC$，$r\lt BC$（因为圆与边$AB$相交，半径不能超过直角边长度）。
已知$CD = 2.4cm$，$AC = 3cm$，$BC = 4cm$，所以$2.4\lt r\leqslant 3$。
（3）若边$AB$与$\odot C$只有一个公共点
当直线与圆只有一个公共点时，直线与圆相切，此时$r = d$（$d$为圆心$C$到直线$AB$的距离，即$CD$的长度），即$r = 2.4cm$；
当圆与$AC$或$BC$相切时，也只有一个公共点，此时$3\lt r\leqslant 4$。
综上，$r = 2.4$或$3\lt r\leqslant 4$。
【答案】：
(1)$0\lt r\lt 2.4$；
(2)$2.4\lt r\leqslant 3$；
(3)$r = 2.4$或$3\lt r\leqslant 4$