第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
20. 根据以下材料,探索完成任务.
【材料1】某水果店购进某种桃子,保质期为30天,每箱桃子的售价为100元.
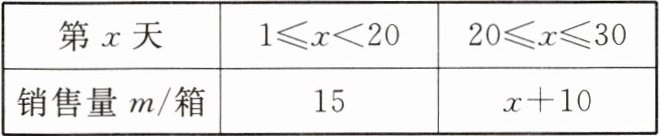
【材料2】设桃子第x天的销售量为m箱,m与x之间的关系如下表所示:
| 第x天 | $1\leq x<20$ | $20\leq x\leq30$ |
| 销售量m/箱 | 15 | $x+10$ |
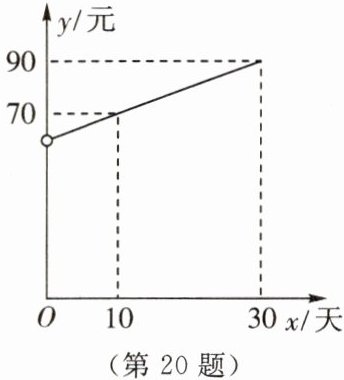
【材料3】由于桃子需要冷藏保存,因此成本也会逐日增加,每箱桃子的成本为y元,y与x的函数关系如图所示.
(1)求每箱桃子的成本y(元)关于x的函数解析式.
(2)若桃子每天的销售利润为W元,求W关于x的函数解析式,并求出第几天的销售利润最大?最大销售利润是多少元?
【材料1】某水果店购进某种桃子,保质期为30天,每箱桃子的售价为100元.
【材料2】设桃子第x天的销售量为m箱,m与x之间的关系如下表所示:
| 第x天 | $1\leq x<20$ | $20\leq x\leq30$ |
| 销售量m/箱 | 15 | $x+10$ |

【材料3】由于桃子需要冷藏保存,因此成本也会逐日增加,每箱桃子的成本为y元,y与x的函数关系如图所示.

(1)求每箱桃子的成本y(元)关于x的函数解析式.
(2)若桃子每天的销售利润为W元,求W关于x的函数解析式,并求出第几天的销售利润最大?最大销售利润是多少元?
答案:
(1)解:设$y=kx+b$,由图知函数过点$(10,70)$,$(30,90)$。
$\begin{cases}10k+b=70\\30k+b=90\end{cases}$,解得$\begin{cases}k=1\\b=60\end{cases}$
当$x=0$时,$y=60$,所以$y=x+60$,$1\leq x\leq30$。
(2)解:售价为100元/箱,利润$W=m(100 - y)$。
当$1\leq x<20$时,$m=15$,$y=x+60$,
$W=15(100 - (x + 60))=15(40 - x)=-15x + 600$,
此时$W$随$x$增大而减小,$x=1$时,$W_{max}=-15×1 + 600=585$。
当$20\leq x\leq30$时,$m=x + 10$,$y=x + 60$,
$W=(x + 10)(100 - (x + 60))=(x + 10)(40 - x)=-x^2 + 30x + 400$,
对称轴$x=15$,开口向下,在$20\leq x\leq30$上$W$随$x$增大而减小,
$x=20$时,$W=-400 + 600 + 400=600$。
比较$585$与$600$,第20天利润最大,最大利润600元。
综上,$W=\begin{cases}-15x + 600(1\leq x<20)\\-x^2 + 30x + 400(20\leq x\leq30)\end{cases}$,第20天利润最大,为600元。
(1)解:设$y=kx+b$,由图知函数过点$(10,70)$,$(30,90)$。
$\begin{cases}10k+b=70\\30k+b=90\end{cases}$,解得$\begin{cases}k=1\\b=60\end{cases}$
当$x=0$时,$y=60$,所以$y=x+60$,$1\leq x\leq30$。
(2)解:售价为100元/箱,利润$W=m(100 - y)$。
当$1\leq x<20$时,$m=15$,$y=x+60$,
$W=15(100 - (x + 60))=15(40 - x)=-15x + 600$,
此时$W$随$x$增大而减小,$x=1$时,$W_{max}=-15×1 + 600=585$。
当$20\leq x\leq30$时,$m=x + 10$,$y=x + 60$,
$W=(x + 10)(100 - (x + 60))=(x + 10)(40 - x)=-x^2 + 30x + 400$,
对称轴$x=15$,开口向下,在$20\leq x\leq30$上$W$随$x$增大而减小,
$x=20$时,$W=-400 + 600 + 400=600$。
比较$585$与$600$,第20天利润最大,最大利润600元。
综上,$W=\begin{cases}-15x + 600(1\leq x<20)\\-x^2 + 30x + 400(20\leq x\leq30)\end{cases}$,第20天利润最大,为600元。
查看更多完整答案,请扫码查看


