《2025年作业本江西教育出版社九年级数学全一册人教版》

9. 为做好消杀工作,某校在专业人员指导下对教室进行“熏药消毒”. 已知在药物燃烧及释放过程中,室内空气中每立方米含药量$y$(mg)与时间$x$(min)之间的关系如图所示(即图中线段$OA和双曲线在A$点及其右侧的部分). 根据图象所示信息,解答下列问题：

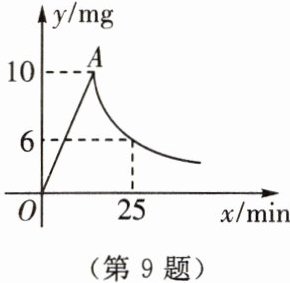
(1)写出从药物释放开始,$y与x$之间的函数关系及自变量的取值范围.
(2)据测定,当空气中每立方米的含药量低于2 mg时,对人体无毒害作用,那么从消毒开始,第几分钟后师生才能进入教室？

答案： 1. （1）
设反比例函数解析式为$y = \frac{k}{x}(k\neq0)$：
把$(25,6)$代入$y=\frac{k}{x}$，得$6=\frac{k}{25}$，解得$k = 150$，所以反比例函数解析式为$y=\frac{150}{x}$。
当$y = 10$时，代入$y=\frac{150}{x}$，得$10=\frac{150}{x}$，解得$x = 15$，所以$A(15,10)$。
设线段$OA$的解析式为$y=mx(m\neq0)$：
把$A(15,10)$代入$y = mx$，得$10 = 15m$，解得$m=\frac{2}{3}$，所以$y=\frac{2}{3}x$。
所以$y$与$x$之间的函数关系为$y=\begin{cases}\frac{2}{3}x(0\leqslant x\leqslant15)\\frac{150}{x}(x\gt15)\end{cases}$。
2. （2）
当$y = 2$时：
代入$y=\frac{150}{x}$（因为$x\gt15$时，$y$随$x$的增大而减小，且$2\lt10$，所以代入反比例函数），得$2=\frac{150}{x}$。
解方程$2x = 150$，解得$x = 75$。
综上，（1）$y=\begin{cases}\frac{2}{3}x(0\leqslant x\leqslant15)\\frac{150}{x}(x\gt15)\end{cases}$；（2）第$75$分钟后师生才能进入教室。