《2025年初中同步练习册分层卷九年级数学上册人教版》

8. (3 分)如图, 在平面直角坐标系中, 边长为 2 的正六边形 $ ABCDEF $ 的中心与原点 $ O $ 重合, $ AB // x $ 轴, 将六边形绕点 $ O $ 逆时针旋转, 每次旋转 $ 90^{\circ} $, 则第 2026 次旋转结束时, 点 $ B $ 的坐标为 (B)

A.$ (\sqrt{3}, -1) $
B.$ (-1, -\sqrt{3}) $
C.$ (-\sqrt{3}, 1) $
D.$ (1, \sqrt{3}) $

答案： B

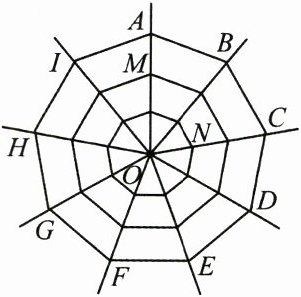
9. (3 分)一个蜘蛛网如图所示, 若多边形 $ ABCDEFGHI $ 为正九边形, 其中心点为点 $ O $, 点 $ M $, $ N $ 分别在射线 $ OA $, $ OC $ 上, 则 $ \angle MON = $ 80°. (填度数)

答案： 80°

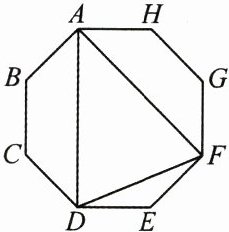
10. (3 分)(2025·武汉质检)如图, 在正八边形 $ ABCDEFGH $ 中, $ AB = 2 $, 连接 $ AD $, $ AF $, $ DF $, 则 $ \triangle ADF $ 的面积为 ____.

答案：
4+3 $\sqrt{2}$ 解析：如图，连接 BG，CF，分别交 AD 于点 M，N.

在正八边形 ABCDEFGH 中，可得 BG⊥AD，CF⊥AD.
∵正八边形每个内角为 $\frac{(8-2)×180°}{8}$=135°，
∴∠ABM=45°.
∴MA=MB= $\frac{\sqrt{2}}{2}$AB= $\sqrt{2}$.
同理，CN=DN= $\sqrt{2}$，
∴AD=2+2 $\sqrt{2}$.
∴CF=AD=2+2 $\sqrt{2}$.
∴FN=2+ $\sqrt{2}$.
∴△ADF 的面积= $\frac{1}{2}$×(2+2 $\sqrt{2}$)×(2+ $\sqrt{2}$)=4+3 $\sqrt{2}$.

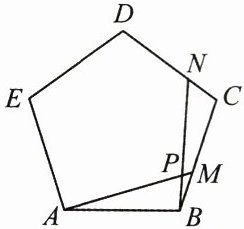
11. (8 分)(2025·商洛商南县期中)如图, 点 $ M $, $ N $ 分别是正五边形 $ ABCDE $ 的边 $ BC $, $ CD $ 上的点, 且 $ BM = CN $, $ AM $ 交 $ BN $ 于点 $ P $.
(1)求证: $ AM = BN $;
(2)求 $ \angle APN $ 的度数.

答案：
(1)证明：
∵五边形 ABCDE 为正五边形，
∴AB=BC，∠ABM=∠C.
在△ABM 和△BCN 中，
$\begin{cases} AB=BC, \\ ∠ABM=∠C, \\ BM=CN, \end{cases}$
∴△ABM≌△BCN(SAS).
∴AM=BN.
(2)解：
∵△ABM≌△BCN，
∴∠BAM=∠CBN.
∵∠BAM+∠ABP=∠APN，
∴∠CBN+∠ABP=∠APN=∠ABC= $\frac{(5-2)×180°}{5}$=108°.
∴∠APN 的度数为 108°.

12. (13 分)如图, 正方形 $ ABCD $ 内接于 $ \odot O $, $ E $ 为 $ \overset{\frown}{AD} $ 的中点.
(1)作等边三角形 $ EFG $, 使点 $ F $, $ G $ 分别在 $ \overset{\frown}{AB} $ 和 $ \overset{\frown}{CD} $ 上; (用直尺和圆规作图, 保留作图痕迹, 不写作法)
(2)在 (1) 的条件下, 求 $ \angle BOG $ 的度数;
(3)若正方形 $ ABCD $ 的边长为 4, 求 (1)中等边三角形 $ EFG $ 的边长.

答案：

(1)如图，连接 EO 并延长，交⊙O 于点 H，以点 H 为圆心、HO 为半径画圆，交⊙O 于点 F，G，点 F，G 即为所求.

(2)如图，连接 OB，OG.
∵△EFG 是等边三角形，
∴EH⊥GF.
∴∠GOH=2∠GEH=2×30°=60°.
∵四边形 ABCD 是正方形，
∴∠BOH=45°.
∴∠BOG=∠BOH+∠GOH=45°+60°=105°.
(3)如图，连接 OF，OB，过点 O 作 ON⊥EF 于点 N.

∵OM⊥BC，
∴BM= $\frac{1}{2}$BC= $\frac{1}{2}$×4=2.
在 Rt△BOM 中，OM=2，
∴OB=2 $\sqrt{2}$.
在 Rt△FON 中，∠OFN=30°，OF=2 $\sqrt{2}$，
∴ON= $\sqrt{2}$.
∴FN= $\sqrt{(2\sqrt{2})^2 - (\sqrt{2})^2}$= $\sqrt{6}$.
∴EF=2 $\sqrt{6}$.
∴等边三角形 EFG 的边长为 2 $\sqrt{6}$.