《2025年初中同步练习册分层卷九年级数学上册人教版》

8. (3分)(2024·牡丹江中考)如图, 四边形 $ABCD$ 是 $\odot O$ 的内接四边形, $AB$ 是 $\odot O$ 的直径, 若 $\angle BEC = 20^{\circ}$, 则 $\angle ADC$ 的度数为 (B)

A.$100^{\circ}$
B.$110^{\circ}$
C.$120^{\circ}$
D.$130^{\circ}$

答案： B

9. (3分)(2024·济宁中考)如图, 分别延长圆内接四边形 $ABCD$ 的两组对边, 延长线相交于点 $E$, $F$.若 $\angle E = 54^{\circ}41'$, $\angle F = 43^{\circ}19'$, 则 $\angle A$ 的度数为 (C)

A.$42^{\circ}$
B.$41^{\circ}20'$
C.$41^{\circ}$
D.$40^{\circ}20'$

答案： C

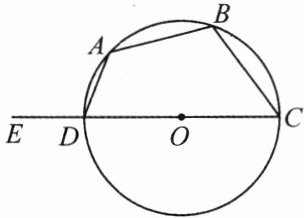
10. (3分)(2024·西宁中考)如图, 四边形 $ABCD$ 内接于 $\odot O$, $E$ 为直径 $CD$ 延长线上一点, $\overset{\frown}{AB} = \overset{\frown}{BC}$, $\angle ADE = 110^{\circ}$, 则 $\angle DAB = $125°.(填度数)

答案： 125°

11. (10分)如图, 四边形 $ABCD$ 内接于 $\odot O$, $F$ 是 $\overset{\frown}{CD}$ 上一点, 且 $\overset{\frown}{DF} = \overset{\frown}{BC}$, 连接 $CF$ 并延长交 $AD$ 的延长线于点 $E$, 连接 $AC$.
(1)若 $\angle B = 125^{\circ}$, $\angle BAC = 25^{\circ}$, 求 $\angle E$ 的度数;
(2)若 $\odot O$ 的半径为 $6$, 且 $\angle B = 2\angle ADC$, 求 $AC$ 的长.

答案：
解：
(1)
∵四边形ABCD内接于⊙O，∠B =125°，
∴∠ADC=180°-∠ABC=180°-125°=55°.
∵$\overset{\frown}{DF}=\overset{\frown}{BC}$，∠BAC=25°，
∴∠DCE=∠BAC=25°.
∴∠E=∠ADC-∠DCE=55°-25°=30°.
(2)如图，连接AO，CO，过点O作OH⊥AC于点H，则AO=CO=6.

∵四边形ABCD内接于⊙O，
∴∠B+∠ADC=180°.
∵∠B=2∠ADC，
∴∠ADC =60°，∠B=2∠ADC=120°.
∴∠AOC=2∠ADC=120°.
∵OA=OC，
∴∠OAC=∠OCA=$\frac{1}{2}$(180°-∠AOC)=30°.
∵AO=6，OH⊥AC，
∴OH=$\frac{1}{2}$AO=3.
由勾股定理，得AH=$\sqrt{AO^2-OH^2}$=$\sqrt{6^2-3^2}=3\sqrt{3}$.
∵OH⊥AC，OH过圆心O，
∴AH=CH=3$\sqrt{3}$.
∴AC=AH+CH=6$\sqrt{3}$.

12. (15分)如图, 两个等圆 $\odot O_{1}$ 和 $\odot O_{2}$ 相交于 $A$, $B$ 两点, 经过点 $A$ 的直线与两圆分别交于点 $C$, $D$, 经过点 $B$ 的直线与两圆分别交于点 $E$, $F$, 且 $CD // EF$.求证:
(1)四边形 $CEFD$ 是平行四边形;
(2)$\overset{\frown}{CE} = \overset{\frown}{DF}$.

答案：
证明：
(1)如图，连接AB.

∵四边形ABEC是⊙O₁的内接四边形，
∴∠BAD=∠E.
又
∵四边形ADFB是⊙O₂的内接四边形，
∴∠BAD+∠F=180°.
∴∠E+∠F=180°.
∴CE//DF.
∵CD//EF，
∴四边形CEFD是平行四边形.
(2)由
(1)得四边形CEFD是平行四边形，
∴CE=DF.
∴$\overset{\frown}{CE}=\overset{\frown}{DF}$.