《2025年初中同步练习册分层卷九年级数学上册人教版》

1. (3 分)(2025·南宁期中)已知$\odot O$的半径是 6,圆心到直线$l的距离d = 5$,则直线$l与圆O$的位置关系是 (C)
A.相离
B.相切
C.相交
D.无法判断

答案： C

2. (3 分)在平面直角坐标系中,以点$A(2,1)$为圆心、1 为半径的圆与$y$轴的位置关系是 (A)
A.相离
B.相切
C.相交
D.不确定

答案： A

3. (3 分)(2025·武汉质检)在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB = 8$,$AC = 6$,以点$A$为圆心、长度 5 为半径的圆与直线$BC$的公共点的个数为2.

答案： 2

4. (6 分)如图,正方形$ABCD$的边长为 2,$AC和BD相交于点O$,过点$O作EF// AB$,交$BC于点E$,交$AD于点F$,则以点$B$为圆心、$\sqrt{2}长为半径的圆与直线AC$,$EF$的位置关系分别是什么？

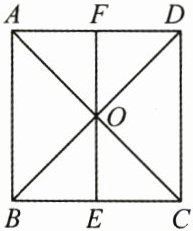
答案： 解：由题中已知条件，得 BO⊥AC，BO = $\frac{1}{2}BD=\frac{1}{2}\sqrt{BC^{2}+CD^{2}}=\sqrt{2}$，即点 B 到 AC 的距离为$\sqrt{2}$，与$\odot B$的半径相等。
∴直线 AC 与$\odot B$相切。
∵EF//AB，∠ABC = 90°，
∴BE⊥EF，垂足为 E，且$BE=\frac{1}{2}BC=\frac{1}{2}×2 = 1＜\sqrt{2}$。
∴直线 EF 与$\odot B$相交。

5. (3 分)若直线$a$与半径为 4 的$\odot O$相交,则圆心$O到直线a$的距离可能为(A)
A.3
B.4
C.4.5
D.5

答案： A

6. (3 分)在直角坐标平面内,已知点$M(4,3)$,以点$M$为圆心、$r为半径的圆与x$轴相交,与$y$轴相离,那么$r$的取值范围为 (D)
A.$0 ＜ r ＜ 5$
B.$3 ＜ r ＜ 5$
C.$4 ＜ r ＜ 5$
D.$3 ＜ r ＜ 4$

答案： D

7. (3 分)(2024·四平伊通县期末)已知矩形$ABCD$中,$AB = 4$,$BC = 3$,以点$B$为圆心、$r$为半径作圆,且$\odot B与边CD$有唯一公共点,则$r$的取值范围是3≤r≤5.

答案： 3≤r≤5

8. (6 分)已知$\odot O的半径r = 7\mathrm{cm}$,直线$l_{1}// l_{2}$,且$l_{1}与\odot O$相切,圆心$O到l_{2}的距离为9\mathrm{cm}$.求$l_{1}与l_{2}之间的距离m$.

答案：
解：有两种情况：如图，当$l_{2}$与$l_{1}$在圆的同一侧时，
m = 9 - 7 = 2(cm)。
当$l_{2}$与$l_{1}$在圆的两侧时，
m = 9 + 7 = 16(cm)。

9. (3 分)(2025·无锡江阴市质检)如图,在$\triangle ABC$中,$AB = 6$,$AC = 8$,$BC = 10$,$D$,$E分别是AC$,$AB$的中点,则以$DE为直径的圆与BC$的位置关系是 ( )


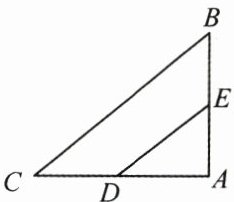
A.相切
B.相交
C.相离
D.无法确定

答案：
B 解析：如图，过点 A 作 AM⊥BC 于点 M，交 DE 于点 N。

∵AB = 6，AC = 8，BC = 10，
∴∠CAB = 90°。
∴AM·BC = AC·AB。
∴$AM=\frac{6×8}{10}=4.8$。
∵D，E 分别是 AC，AB 的中点，
∴DE//BC，$DE=\frac{1}{2}BC = 5$。
∴$AN = MN=\frac{1}{2}AM$。
∴MN = 2.4。
∵以 DE 为直径的圆的半径为 2.5，
∴r = 2.5 ＞ 2.4。
∴以 DE 为直径的圆与 BC 的位置关系是相交。